Geometria - dowód
AHQ: Wykaż, że w dowolnym trapezie o prostopadłych ramionach odcinek łączący środki jego podstaw
jest równy połowie różnicy ich długości.
5 mar 14:37
salamandra: Podziel na dwa trapezy, wyznacz wysokość (wysokość całego trapezu jako 2h, a tych małych jako
h), przyrównaj sumę pół dwóch małych do dużego
5 mar 14:48
janek191:
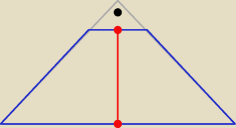
5 mar 14:50
ite:
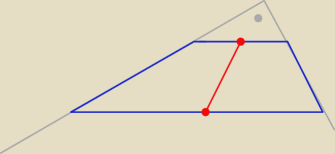
A dowolny to nie taki?
5 mar 14:53
AHQ: @ite Oczywiście, że taki

Dowolne zawsze są nieładne

5 mar 15:21
Saizou :
AHQ może jakiś twój pomysł?
5 mar 15:22
Saizou :
Po pierwsze nie jest to prawdę, wiec jak masz to pokazać ?

5 mar 15:25
Mila:
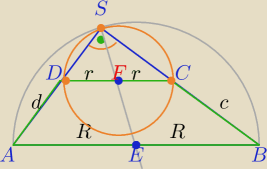
d=2R−2r − różnica podstaw trapezu ABCD
1) |DF|=|FC|=|SF|=r − ponieważ środkowa poprowadzona do przeciwprostokątnej w ΔDCS jest
równa promieniowi okręgu opisanego na tym Δ.
2)| AE|=|EB|=|SE|=R uzasadnienie j.w.
cnw.
5 mar 15:56
Saizou :
jasne
Mila, ubzdurałem sobie, że chodzi o różnice długość ramion

5 mar 16:02
Mila:
Cześć. Czasem też czegoś nie doczytam i głupoty piszę

5 mar 16:11
AHQ: Dzięki

5 mar 16:23
jc: Saizou, też tak zrozumiałem zrozumiałem (różnica mogła przecież dotyczyć ramion).
5 mar 16:23
Saizou :
cóż, trochę niefortunnie sformułowane zadanie

5 mar 16:41
a@b:
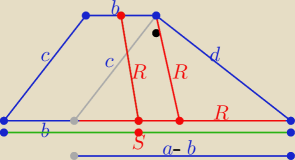
5 mar 17:02
AHQ: a@b −Również dzięki

5 mar 18:37
Biba1000:
8 mar 18:15

 A dowolny to nie taki?
A dowolny to nie taki?
 Dowolne zawsze są nieładne
Dowolne zawsze są nieładne 

 d=2R−2r − różnica podstaw trapezu ABCD
1) |DF|=|FC|=|SF|=r − ponieważ środkowa poprowadzona do przeciwprostokątnej w ΔDCS jest
równa promieniowi okręgu opisanego na tym Δ.
2)| AE|=|EB|=|SE|=R uzasadnienie j.w.
d=2R−2r − różnica podstaw trapezu ABCD
1) |DF|=|FC|=|SF|=r − ponieważ środkowa poprowadzona do przeciwprostokątnej w ΔDCS jest
równa promieniowi okręgu opisanego na tym Δ.
2)| AE|=|EB|=|SE|=R uzasadnienie j.w.





