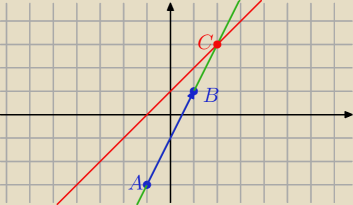
Matematyka geometria analityczna Mk: Dana jest prosta k o równaniu y=x + 1 oraz punkty A=(−1, −3) I B=(1,1). Wyznacz liczbę t taką że wektor AC=wektor AB razy t wiedząc że punkt C należy do prostej k.

janek191:

	1 − (−3)
a =		= 2
	1 −(−1)

y = 2 x + k i B = ( 1, 1) 1 = 2*1 + k ⇒ k = − 1 y = 2 x − 1 x + 1 = 2 x − 1 x = 2 y = 2*2 −1 = 3 C = ( 2, 3) → → AC = [ 2 − (−1), 3 − (−3)] = [ 3, 6 ] = t*AB = t*[ 2, 4] t = 1,5 =====