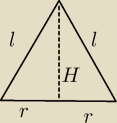
stereometria salamandra: Wykaż, że nie istnieje stożek, w którym stosunek pola powierzchni bocznej do pola jego przekorju osiowego równy jest π H²+r²=l² H=√l²−r² P=r*√l²−r² Pb=πrl

πrl
r*√l2−r2

Jak to teraz ubrać w słowa żeby to wykazać, o ile to jest w ogole dobrze?

wredulus_pospolitus:

	π*rl		l
no i wykaż, że		≠ π czyli że		≠ 1
	r√l2 − r2		√l2−r2

czyli, że l ≠ √l² − r² ... i ciągniesz to dalej

salamandra: No i powiem Ci, że to dobre pytanie, dlaczego l≠ √l²−r², jak to wykazać

wredulus_pospolitus: bo r>0 .więc l² − r² < l² ... więc √l² − r² < √l² = l (bo l > r > 0)

wredulus_pospolitus: więc dowód tego zadania powinien wyglądać tak: r > 0 r² > 0 − r² < 0 l² − r² < l² (warunek na l: l > r , potrzebny później ) √l² − r² < √l² √l² − r² < l

	l
1 <
	√l2−r2

	rl
1 <
	r√l2−r2

	πrl
π <
	r√l2−r2

	Pb		Pb
π <		czyli		≠ π
	Pprzekroju		Pprzekroju

c.n.w.

salamandra: dzięki