prawdodpobieństwo salamandra: Oblicz ile jest możliwości wyboru z grupy liczącej dziesięc osób delegacji składającej się z dwóch osób dlaczego to nie będzie po prostu 10*9, tylko widzę jakiś wzór liczba wyboru 2−osobowej delegacji=U{liczba wszystkich mozliwosci wyboru 2−osobowej delegacji}{liczba kolejności w jakiej 2 osoby zostały wybrane}? Skąd to się wzięło?

Leszek: Sa to dwuelementowe kombinacje ze zbioru dziesiecioelementowego czyli : 10*9 = 90 Chyba , ze jeszcze jest podany jakis warunek ?

wredulus_pospolitus: bo delegacja: (Janek, Franek) oraz (Franek, Janek) to ta sama delegacja, czyż nie

wredulus_pospolitus: gdyby było jeszcze podane, że jeden z nich będzie robił za przełożonego drugiego, to bym się zgodził, ale tak −−− to co za różnica czy jako pierwszego wybierzesz Janka czy Franka?

wmboczek: jeśli osoby nie mają jakieś funkcji w tej delegacji, to kolejność ich wyboru nie ma znaczenia 10*9 szef i zastępca 10*9/2 równorzędni pracownicy

salamandra: Właśnie tak jak wredulus mówisz, ale nie wiem skąd to wynika, że trzeba podzielić przez 2*1

Saizou : Ustawiasz sobie tych ludzi w ciąg: człowiek A, człowiek B (w skrócie AB) ale para AB to ta sama para co BA Dlatego dzielisz przez 2

salamandra: A dlaczego przy trzyosobowej dzielę przez 6?

Saizou : No bo będziesz liczyć trójki ABC ACB BAC BCA CAB CBA razem 3!=6 przypadków

salamandra: tylko hm, dlaczego na przykład nie odejmuję, tylko dzielę?

wredulus_pospolitus: salamandra bo dzielisz przez permutację 'n' elementową Powiedzmy, że z tych 10 osób robimy delegację 4 osobową.

10*9*8*7
	<−−− dzielisz przesz permutację 4−elementową.
4!

ponieważ każda permutacja z elementów ABCD w liczniku jest liczona jako oddzielne zdarzenie, a tak być nie powinno.

salamandra: Wybaczcie, tak jak napisałem, dzis miałem pierwsza lekcje z prawdopobienstwa, stąd takie może durne pytania

Jerzy: To dwuelementowe kombinacje zbioru dziesięcioelementowego:

10 2		10!		8!*9*10
	=		=		= 45
		2!8!		2*8!

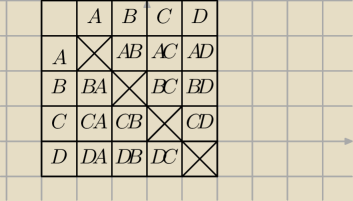
Saizou : Ograniczmy to sobie aby zrozumieć mamy zbiór {A, B, C, D}, masz wybrać dwie osoby do delegacji a) jeśli kolejność jest ważna to masz takich par 4*3=12 (patrz tabelka) b) jeśli kolejność nie jest ważna, to każdą parę liczymy dwukrotnie pary liczone 2 razy to pary typu (AB, BA), (CD,DC), (CA, AC) itd. czyli wynik z a) musisz podzielić na 2=2! Analogicznie możesz rozrysować sobie dla trójek, ale wtedy otrzymasz sześcian i będzie już czytelne.

Jerzy: Jeśli z 10 osób masz wybrać 3 osobową delegację , liczysz trzyelementowe kombinacje

	10 3		10!		7!*8*9*10		8*9*10
zbioru 10 elementowego:		=		=		=		= 120
			3!7!		3!7!		6

salamandra: To chyba jeszcze przede mna, No nic, dzięki Wam. Mam nadzieje, ze to załapie w miarę szybko, bo chce zacząć cokolwiek powtarzać, a nie siedzieć ciagle w nowym materiale