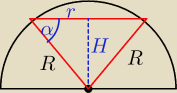
stereometria salamandra: Zadanie: W półkulę o promieniu długości R wpisano stożek, którego wierzchołek leży w środku kuli, a podstawa jest równoległa do podstawy półkuli. a) przedstaw objętość tego stożka jako funkcję kąta nachylenia tworzącej do płaszczyzny jego podstawy * b) wyznacz długość promienia podstawy stożka, przy którym jego objętość jest maksymalna i oblicz tę objętość. na razie a)

	r
cosα=
	R

r=R*cosα

	H
sinα=
	R

H=R*sinα

	1
V=		*π*(R*cosα)2*R*sinα
	3

	π*R2*cos2α*R*sinα		π*R3*cos2α*sinα
V=		=
	3		3

o to chodziło?

Patryk: To zadania z Kiełbasy?

salamandra: nie, z "Księgi Mądrości" mojego nauczyciela

Patryk: Ale Kiełbasę też robisz, prawda?

salamandra: Nie mam na razie czasu, zrobiłem może z 30 zadań, za dużo nauczyciel zadaje na bieżąco zdającym rozszerzenie

Patryk: U mnie z klasy to wszyscy leżą z matmą, mają problemy z zadaniami z podstawy i nauczycielka robi lekcje jakby pod podstawę mimo, że 3/4 osób zadeklarowało rozsz. matmę I przypuszczam, że ja jedyny uczę sie do rozszerzenia, ale kurcze za dużo tego materiału troszkę

salamandra: No u mnie 9 osób i zadania z tej książki co nam daje to widzisz jakie są, że bez pomocy tutaj bym leżał i kwiczał, a mówi, że trudniejsze to dopiero przed nami. Dzisiaj zaczęliśmy rachunek prawdopobieństwa.

salamandra: b) H²+r²=R² H²−R²=−r² R²−H²=r² r=√R²−H²

	π
V=		*(R2−H2)*H
	3

	π
V=		*R2H−H3
	3

f(H)=R²H−H³ f(H)=−H³+R²H f'(H)=−3H²+R² −3H²+R²=0 3H²=R²

	R2
H2=
	3

	R2		R2
H=√		v H=−√
	3		3

	R		R√3		R√3
H1=		=		v H2=−
	√3		3		3

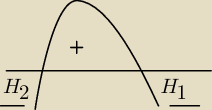
Pochodna mniejsza od zera w przedziale (−∞; H₂), w H₂ zmienia znak więc tam osiąga minimum Większa od zera w przedziale (H₂; H₁), więc tam funkcja rośnie, zmienia znak w H₁ więc tam osiąga maksimum Mniejsza od zera w przedziale (H₁;∞) więc tam funckja maleje

	R2		2R2		R√2		R√6
r=√R2−H2, więc r=√R2−		= √		=		=
	3		3		√3		3

dobrze?..

salamandra: Mógłby ktoś potwierdzić wynik? Muszę mieć pewność, że jest dobrze