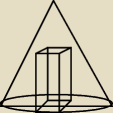
stożek hubik: W stożek obrotowy o promieniu podstawy długości R i wysokości długości H wpisany jest prostopadłościan, którego jedna podstawa, znajduje się na podstawie stożka, a wierzchołki drugiej na powierzchni bocznej stożka. Stosunek długości krawędzi podstawy prostopadłościanu jest równy 2. Oblicz długości krawędzi prostopadłościanu, tak aby jego objętość była największa. Nie jestem pewien co do swoich wyników, więc proszę o bezlitosną krytykę krawędzie podstawy, to kolejno a i b. Wysokość prostopadłościanu to h

a
	=2
b

a = 2b

	h
Do tego trójkąty podobne		={H}{R}
	x

	Hx
h =
	R

Gdzie x to odległość od wierzchołka podstawy prostopadłościanu, do powierzchni bocznej stożka Więc:

	d
x = R −
	2

d − przekątna podstawy d = √a²+b² d = √5a² d = a√5

	a√5
x = R −
	2

	2HR − aH√5
h=
	2R

	a2(2HR−aH√5)
V =
	R

V(a) = 2HRa² −Ha³√5 V'(a) = 4HRa − 3√5a²

	4√5R
a1 = 0 a2 =
	15

a_max = a₂ I resztę z tego wyliczyłem