stereometria
salamandra:
Zadanie:
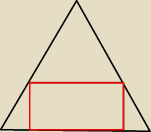
w stożek obrotowy o promieniu podstawy długości R i wysokości długości H wpisany jest
prostopadłościan w ten sposób, że jego podstawa zawarta jest w podstawie stozka, a wierzchołki
drugiej podstawy należą do powierzchni bocznej stożka. Stosunek dlugosci krawędzi podstawy
prostopadłościanu jest równy 2. Oblicz długość krawędzi prostopadłościanu o największej
objętości.
Dobry rysunek przekroju? to, że podstawa prostopadłościanu zawarta jest w podstawie stożka, to
nie znaczy, że ma obejmować ją całą prawda?
4 mar 14:17
jc: Zależy, jak patrzysz. Gdy ściana prostopadłościanu jest do Ciebie równoległa, to widzisz
coś innego.
Spójrz lepiej z góry. Górna ściana, czyli prostokąt, jest wpisana w okrąg.
4 mar 14:45
salamandra:
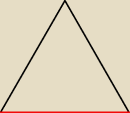
no tak, rozumiem, chodziło mi o to, czy takie coś nie musi być, ale raczej nie może i to głupie
moje pytanie:
(w tym sensie czy ma cały okrąg obejmować, ale jak mam zmieścić teraz pozostałe boki?)
4 mar 14:52
jc:
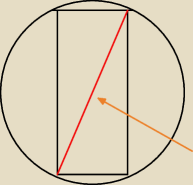
Obrazek, jaki narysowałeś, zobaczysz patrząc prostopadle do przekątnej.
4 mar 15:02
salamandra: Mówisz o tym pierwszym?
4 mar 15:04
Mila:
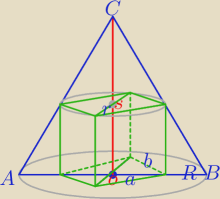
a=2b
4 mar 15:07
salamandra: Dziękuję, czyli dobrze myślałem.
nie rozumiem tego "Stosunek dlugosci krawędzi podstawy
prostopadłościanu jest równy 2"
Ale stosunek dlugosci krawedzi podstawy prostopadłościanu do czego?
4 mar 15:08
Mila:
a, b −krawędzie podstawy prostopadłościanu
4 mar 15:17
salamandra: a dobra, nieważne, ja na to patrzyłem jak na prostokąt

biorę się za rozwiązywanie
4 mar 15:21
salamandra: Patrząc na rysunek Mili
2b=a
h− wysokość prostopadłościanu
(2b)
2+b
2=(2r)
2
4b
2+b
2=4r
2
5b
2=4r
2
Hr=RH−Rh
Ma sens w ogóle to co teraz zrobiłem?
4 mar 15:36
Mila:
Jak najbardziej , oblicz h i naprzód.
4 mar 15:59
salamandra:
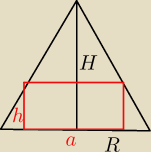
troche inaczej zrobiłem, stosując przekrój
HR−hR=H*{1}{2}a
b=2a
Pp=a*2a=2a
2
| | 2HR−2hR | |
V=2*( |
| )2*h itd, jest to ok? |
| | H | |
4 mar 16:03
salamandra: cd.
f(h)=4H
2R
2h−8HR
2h
2+4R
2h
3
f(h)=4R
2h
3−8HR
2h
2+4H
R2h
f'(h)=12R
2h
2−16HR
2h+4H
2R
2
f'(h)=0 ⇔ 12R
2h
2−16HR
2h+4H
2R
2 =0
12R
2h
2−16HR
2h+4H
2R
2 =0 / : 4
3R
2h
2−4HR
2h+H
2R
2
Δ=16H
2R
4−12R
4H
2=4R
4H
2
√Δ=2R
2H
| | 16HR2−2R2H | | 14H | | 7H | |
h1= |
| = |
| = |
| |
| | 24R2 | | 24 | | 12 | |
4 mar 16:19
salamandra: ale coś mi tu nie gra, więc wracam do tamtego:
cd. 15:36
2b=a
| | 2√5r | | 4√5r | | 8 | |
Pp= |
| * |
| = |
| r2 |
| | 5 | | 5 | | 5 | |
f(r)=−8Hr
3+8RHr
2
f'(r)=−24Hr
2+16RHr
−8Hr(3r−2R)=0
r=0 v 3r=2r
4 mar 16:53
Mila:
16:03 źle
Później napiszę. Zostaw na razie.
4 mar 17:09
salamandra: Powinno być ok, bo kolega ma identyczny wynik, ale czekam

4 mar 17:11
Mila:
16:53 Dobrze.
Jednak napiszę wszystko, nie dałeś ograniczeń, a miałeś różnice.
4 mar 17:12
salamandra: Nie czuję tych zadań, wybacz

4 mar 17:13
Mila:
16:19 jest źle.
4 mar 17:14
salamandra: | | 1 | |
To już wiem, nie potrafię sobie wyobrazić dlaczego np. to nie może być |
| a to co tam |
| | 2 | |
wziąłem, gdzie będą w ogóle punkty styku, jak wpaść na to, że ta podstawa prostopadłościanu
tam na górze to prostokąt wpisany w okrąg, jak narysować przekrój czegoś takiego, no porażka
totalna... mimo że mi wyszło, ale wyliczyć to nie problem
4 mar 17:16
Mila:
Nie szalej, masz drobne usterki. To zadanie należy do trudnych.
Wytłumaczę, ale później, teraz nie mogę

Rozwiązuj następne zadania.
4 mar 17:19
Mila:
cd. po 15:36
2)
| | H | |
V(b)= |
| *(2Rb2−b3√5) (H/R− stała wielkość, b zmienna) |
| | R | |
Teraz analizuj pochodną i napisz gdzie i dlaczego jest V
max
4 mar 17:44
salamandra:
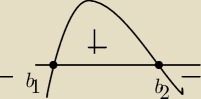
−3b
2√5+4Rb=0
−b(3b
√5−4R)=0
b1=0 v 3b
√5=4R
Pochodna mniejsza od zera w przedziale (−
∞;b1), zmienia znak w b1, więc tam osiąga wartośc min,
Pochodna większa od zera w przedziale (b1;b2), więc tam funkcja rośnie, zmienia znak w b2, więc
tam osiąga wartość max
Pochodna mniejsza od zera w przedziale (b2;
∞), więc tam funkcja maleje
To jest akurat łatwe, gorzej z wyobraźnią i tym co napisałem.
4 mar 17:53
Mila:
Teraz patrz na rysunek i kształtuj wyobraźnię. Będzie dobrze.

4 mar 18:18
salamandra: Dziękuję Milu

4 mar 20:19
 Zadanie:
w stożek obrotowy o promieniu podstawy długości R i wysokości długości H wpisany jest
prostopadłościan w ten sposób, że jego podstawa zawarta jest w podstawie stozka, a wierzchołki
drugiej podstawy należą do powierzchni bocznej stożka. Stosunek dlugosci krawędzi podstawy
prostopadłościanu jest równy 2. Oblicz długość krawędzi prostopadłościanu o największej
objętości.
Dobry rysunek przekroju? to, że podstawa prostopadłościanu zawarta jest w podstawie stożka, to
nie znaczy, że ma obejmować ją całą prawda?
Zadanie:
w stożek obrotowy o promieniu podstawy długości R i wysokości długości H wpisany jest
prostopadłościan w ten sposób, że jego podstawa zawarta jest w podstawie stozka, a wierzchołki
drugiej podstawy należą do powierzchni bocznej stożka. Stosunek dlugosci krawędzi podstawy
prostopadłościanu jest równy 2. Oblicz długość krawędzi prostopadłościanu o największej
objętości.
Dobry rysunek przekroju? to, że podstawa prostopadłościanu zawarta jest w podstawie stożka, to
nie znaczy, że ma obejmować ją całą prawda?
 no tak, rozumiem, chodziło mi o to, czy takie coś nie musi być, ale raczej nie może i to głupie
moje pytanie:
(w tym sensie czy ma cały okrąg obejmować, ale jak mam zmieścić teraz pozostałe boki?)
no tak, rozumiem, chodziło mi o to, czy takie coś nie musi być, ale raczej nie może i to głupie
moje pytanie:
(w tym sensie czy ma cały okrąg obejmować, ale jak mam zmieścić teraz pozostałe boki?)
 Obrazek, jaki narysowałeś, zobaczysz patrząc prostopadle do przekątnej.
Obrazek, jaki narysowałeś, zobaczysz patrząc prostopadle do przekątnej.
 a=2b
a=2b
 biorę się za rozwiązywanie
biorę się za rozwiązywanie
 troche inaczej zrobiłem, stosując przekrój
troche inaczej zrobiłem, stosując przekrój


 Rozwiązuj następne zadania.
Rozwiązuj następne zadania.
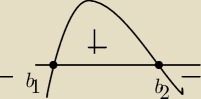 −3b2√5+4Rb=0
−b(3b√5−4R)=0
b1=0 v 3b√5=4R
−3b2√5+4Rb=0
−b(3b√5−4R)=0
b1=0 v 3b√5=4R

