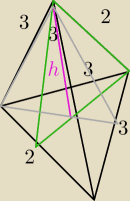
czworościan janusz: W czworościanie o podstawie ABC i wierzchołku S dwie krawędzie AB i CS mają długość 2, a długość każdej z pozostałych krawędzi jest równa 3. Oblicz objętość tego ostrosłupa. Wykorzystałem trójkąt zielony i wyszło mi tak jak w odpowiedziach,natomiast wykorzystując zielony wyszło zupełnie coś innego, wyszły inne wysokości, chyba nie jest to możliwe? Obliczenia sprawdzałem parę razy już.

janusz: wykorzystując szary wyszło zupełnie coś innego*

ite: Jeśli wpiszesz obliczenia, będzie je można sprawdzić.

an: w szarym prawdopodobnie źle policzyłeś wysokość ściany, ona padając na krawędź podstawy nie dzieli jej na pół jak w zielonym

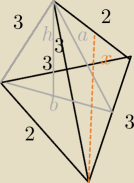janusz: Z tw. Pitagorasa x=2√2 ,pole tego trójkąta=2√2

	3a		4√2
zatem 2√2=		czyli a=
	2		3

b wyjdzie tylko samo co a a trzeci bok jest równy 3 teraz liczę wysokość szarego trójkąta opuszczoną na bok 3 z tw Pitagorasa, wychodzi

	√47		√47
		,czyli pole szarego jest równe
	6		4

√47		4√2   h 3		3√94		√47
	=		,czyli h=		licząc objętość wychodzi V=
4		2		16		4

Pewnie popełniłem jakiś banalny błąd i nie mogę go zauważyć

ite: Wyliczenia są poprawne, ale wysokość czworościanu (różówa) nie jest wysokością szarego trójkąta. https://www.geogebra.org/3d/pkacnyyw

janusz: ok,dzięki że Ci się chciało

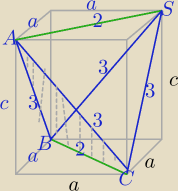Mila: Wpisujemy czworościan w prostopadłościan o podstawie kwadratowej i wysokości c. 1) V_prostop.=a²*c 2²=a²+a² ⇔2a²=4, a²=2 3²=a²+c² ⇔9=2+c² c²=7, c=√7 V_prostop.=2√7 2) Od objętości prostopadłościanu odejmujemy objętość 4 naroży.

	1		1		2
VABCS=2√7−(4*		*		*a2*c)=2√7−		*2*√7
	3		2		3

	2√7
VABCS=
	3

=================