Stereometria Patryk: Cześć, Czy mógłby mi ktoś wytłumaczyć z czego wynika, że ostrosłup z poniższego zadania ma równe krawędzie boczne? Bo już się trochę pogubiłem jeśli chodzi o te długości krawedzi bocznych jeśli ostrosłup nie jest prawidłowy... https://forum.zadania.info/viewtopic.php?t=23233

salamandra: Bo są nachylone pod tym samym kątem

wredulus_pospolitus: wynika z zapisu: wszystkie KRAWĘDZIE nachylone są pod tym samym kątem. Skoro są pod tym samym kątem nachylone to mamy:

	H		H		H
sinα =		=		=
	krawędź 1		krawędź 2		krawędź 3

czyli krawędź 1 = krawędź 2 = krawędź 3

wredulus_pospolitus: Salamandra już to zapamiętał

salamandra: I nawet nie wiesz jak to ułatwiło dalsze rozumienie tematu..

salamandra: Łopatologicznie− zwróć uwagę ze jak są nachylone pod tym samym katem a byłyby rożnej długości to nie „skleiłyby” się we wspólnym punkcie

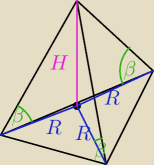
Saizou : Wynika to z faktu, że wszystkie krawędzie nachylone są pod tym samym kątem do płaszczyzny podstawy.

wredulus_pospolitus: Patryk −−− mało tego (co z resztą salamandra też już wie) ... informacja o tym, że wszystkie krawędzie są pod tym samym kątem mówi nam także precyzyjnie gdzie znajduje się spodek wierzchołka tego ostrosłupa (w środku okręgu opisanego na podstawie)

Patryk: W tym przypadku to chyba ściany boczne są nachylone pod tym samym kątem, nie krawędzie ale ta zasada działa w obydwu przypadkach? Jeśli w ostrosłupie krawędzie boczne lub ściany boczne są nachylone pod tym samym kątem do podstawy to krawędzie boczne są tej samej długości?

wredulus_pospolitus: Nie ... w jakim 'tym przypadku'

wredulus_pospolitus: Inaczej wygląda zasada dla krawędziach pod tym samym kątem, a inaczej przy ścianach bocznych pod tym samym kątem

salamandra: Gdy ściany boczne są nachylone pod tym samym katem to spodkiem wysokości będzie środek okręgu wpisanego w podstawę

Patryk: 'tym przypadku' czyli z tego zadania, które podałem w linku Wiem, że jeśli ściany boczne są pod tym samym kątem to uwzględniamy okrąg wpisany w podstawe?

Saizou : krawędzie −> środek okręgu opisanego na trójkącie ściany −> środek okręgu wpisanego w trójkąt

salamandra: Strona 56 Kiełbasę otwieraj, tam masz napisane ładnie Lub jak odgrzebiesz mój wątek niedawno gdzie Mila i wredus mi to rozpisali

Saizou : Podstawą ostrosłupa jest trójkąt prostokątny o przeciwprostokątnej długości c i kącie ostrym α. Wszystkie krawędzie boczne nachylone są do płaszczyzny podstawy pod kątem β. Oblicz pole powierzchni bocznej ostrosłupa.

salamandra: Masz łatwo, bo przeciwprostokątna będzie średnica okręgu opisanego

Patryk: Ten ziomek pomylił się bo powinno być ściany boczne ale w rozwiązaniu poniżej jest poprawnie rozwiązane. W każdym razie podsumowując, zarówno gdy ściany boczne są nachylone pod tym samym kątem albo krawędzie, wtedy krawędzie boczne są równe?

wredulus_pospolitus: jaki 'ten ziomek' W treści zadania są krawędzie ... pytałeś się czemu są równe krawędzie ... więc w TYM zadaniu krawędzie są równe (czyli pod tym samym kątem).

wredulus_pospolitus: Nie ... jak ściany są nachylone pod tym samym kątem to WYSOKOŚCI tychże ścian są sobie równe ... natomiast same krawędzie nie muszą (i poza jednym przypadkiem nawet nie będą) być równe

Patryk: Dobra, to już wiem wszystko co chciałem. Dzięki wielkie za informacje. A z tym ziomkiem chodziło mi o to, że powinien napisa ściany boczne, bo we wskazówce do tego zadania jest napisane, że spodek wysokości jest środkiem okręgu wpisanego w trójkąt Ale Irena z tejże strony zauważyła błąd w treści i rozwiązała zadanie poprawnie