Stereometria
Patryk:
Cześć,
Czy mógłby ktoś sprawdzić czy poprawnie wykonałem obliczenia w tym zadaniu? Bo wynik wychodzi
mi trochę inny niż w odpowiedzi i nie wiem gdzie jest błąd
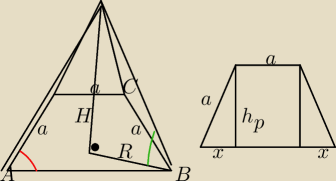
Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym α w którym ramię i krótsza
podstawa ma długośc a. Każda krawędź bocz a ostrosł. tworzy z płaszczyzną podstawy kąt β.
Oblicz objętość ostrosłupa.
Czerwony łuk −> kąt α
Zielony−> kąt β
x
2 + hp
2 = a
2
.......
x = acosα
2.
podstawa dłuższa trapezu:
AB = 2x + a = a(2cosα+1)
| | (2a + 2acosα)*asinα | |
Pp = |
| |
| | 2 | |
.,..... Pp = a
2sinα(cosα+1)
4. Pole trójkąta ABC = 1/2 * Pp = 1/2 * a
2 * sinα(cosα+1)
5. Licze przekątną AC z tw.cosinusów // AB = a(2cosα+1)
AC
2 = (a(2cosα+1))
2 + a
2 − 2a
2(2cosα+1)*cosα
......
AC = a
√2*
√2cosα+1
6.Licze promień okręgu opisanego na trapezie
| | a*AB*AC | |
Pole trójkąta ABC = |
| // wyliczam z tego R |
| | 4*R | |
| | a*√2(2cosα+1)*√cosα+1 | |
R= |
| // a3 skróciło się z a2 z |
| | | |
mianownika
7. tgβ = H / R
| | tgβ*a*√2(2cosα+1)*√cosα+1 | |
H = |
| |
| | 2* sinα(cosα+1) | |
| | tgβa3√2(2cosα+1)√cosα+1 | |
8. objętość V = |
| <−−−−−moja |
| | 6 | |
| | √2a3√(1+cosα)3*tgβ | |
objętość powinna wyjść V = |
| |
| | 6 | |
3 mar 17:31
Saizou :
a jaka jest odpowiedź?
3 mar 17:36
Patryk: napisałem na końcu przecież

3 mar 17:37
Saizou :
Odpowiedź z podręcznika

3 mar 17:37
Patryk: Z podręcznika. Zbiór Kiełbasy

3 mar 17:40
Saizou :
Jaka jest odpowiedź w zbiorze?
Być może masz odpowiedź równoważną.
3 mar 17:41
Saizou :
Sorry, moja wina, nie doczytałem do końca

3 mar 17:43
Saizou :
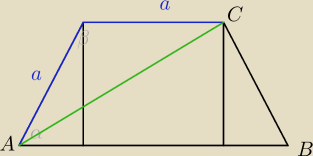
można łatwiej policzyć AC
β=180−α
|AC|
2=a
2+a
2−2a
2cos(180−α)
|AC|
2=2a
2(1+cosα)
|AC|=a
√2*
√1+cosα
i R jest o wiele łatwej z tw. sinusów
3 mar 17:55
Patryk: No w sumie łatwiej

Chociaż muszę mieć gdzieś błąd w obliczeniach bo Tobie wyszła inna
długość AC
3 mar 18:00
Saizou :
Pokaż obliczenia AC, bo nie zapisałeś ich tutaj

3 mar 18:06
Patryk: AC
2 = (a(2cosα+1))
2 + a
2 − 2a
2(2cosα+1)cosα
AC
2 = a
2(2cos+1)
2+a
2 − 2a
2(2cosα+1)cosα
AC
2 = a
2(4cos
2α + 4cosα + 1 +1 − 4cos
2α−2cosα)
AC
2 = a
2(2cosα+2)
AC = a
√2√cosα+1 ........ a nie sorki AC wyszło to samo


zauważyłem przy przepisywaniu
dopiero. W takim razie nie wiem gdzie jest błąd
3 mar 18:16
Saizou :
Z twojego pomysły mamy
|AC|2=(2acosα+a)2+a2−2a(2acosα+a)cosα
|AC|2=4a2cos2α+4a2cosα+a2+a2−4a2cos2α−2a2cosα
|AC|2=2a2cosα+2a2
|AC|2=2a2(cosα+1)
|AC|=a√2√cosα+1
Myślę, że gdzieś popełniłeś błąd przy redukowaniu
3 mar 18:18
Saizou :
Jeśli liczyłeś z błędem, to zmieni Ci się R
3 mar 18:19
Saizou :
| | a√2√1+cosα | |
R= |
| (z tw. sinusów) |
| | 2sinα | |
i potem już z górki
3 mar 18:25
Patryk: Dobra, już nie mam siły analizować tego, możliwe, że gdzieś się wkradła literówka i tyle. W
każdym razie prawie dobrze wyszło. Dzięki za pomoc

Czas na następne zadanka 'tego typu'.
A tak nawiązując do tego zadania i innego, które robię, czy mógłbyś zobrazować na rysunki jakie
sa odcinki dokładnie w trapezie równoramiennym wpisanym w okrąg?
I drugie pytanko, jeśli mam trójkąt prostokątny i poprowadzę środkową od kąta prostego to
środkowa będzie równa połowie przeciwprostokątnej, prawda? Tam wyjdzie trójkąt
równoramienny...
3 mar 18:32
Saizou :
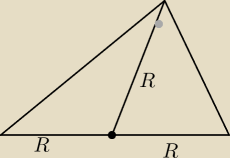
NIe za bardzo wiem, co co CI chodzi z tymi odcinkami w trapezie równoramiennym.
Co do trójkąta prostokątnego.
Środkowa to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
3 mar 18:36
Patryk: W trapezie równoramiennym jedyny sposób na policzenie promienia okręgu opisanego na trapezie
będzie poprzez trójkąt, który jest utworzono z przekątnej trapezu? Bo taka przekątna dzieli
trapez równoramienny na dwa przystające trójkąty, w nim mogę policzyć R z pola lub tw. sinusów
jeśli znam kąt.
3 mar 18:44
Saizou :
Nie jedyny, ale tak jest najłatwiej.
3 mar 18:47
Patryk: Ok, dzięki. To jeszcze jedno pytanko, jeśli mam ostrosłup o podstawie trójkąta równoramiennego,
to krawędzie boczne będa równej długości?
3 mar 19:23
Saizou :
To zależy, czy ostrosłup jest ostrosłupem prostym.
3 mar 19:24
Patryk: Czyli, że jeśli jest prosty to krawędzie boczne ma równe? I to samo się tyczy każdego
ostrosłupa o dowolnej figurze w podstawie?
3 mar 19:28
 Cześć,
Czy mógłby ktoś sprawdzić czy poprawnie wykonałem obliczenia w tym zadaniu? Bo wynik wychodzi
mi trochę inny niż w odpowiedzi i nie wiem gdzie jest błąd
Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym α w którym ramię i krótsza
podstawa ma długośc a. Każda krawędź bocz a ostrosł. tworzy z płaszczyzną podstawy kąt β.
Oblicz objętość ostrosłupa.
Czerwony łuk −> kąt α
Zielony−> kąt β
Cześć,
Czy mógłby ktoś sprawdzić czy poprawnie wykonałem obliczenia w tym zadaniu? Bo wynik wychodzi
mi trochę inny niż w odpowiedzi i nie wiem gdzie jest błąd
Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym α w którym ramię i krótsza
podstawa ma długośc a. Każda krawędź bocz a ostrosł. tworzy z płaszczyzną podstawy kąt β.
Oblicz objętość ostrosłupa.
Czerwony łuk −> kąt α
Zielony−> kąt β




 można łatwiej policzyć AC
β=180−α
|AC|2=a2+a2−2a2cos(180−α)
|AC|2=2a2(1+cosα)
|AC|=a√2*√1+cosα
i R jest o wiele łatwej z tw. sinusów
można łatwiej policzyć AC
β=180−α
|AC|2=a2+a2−2a2cos(180−α)
|AC|2=2a2(1+cosα)
|AC|=a√2*√1+cosα
i R jest o wiele łatwej z tw. sinusów
 Chociaż muszę mieć gdzieś błąd w obliczeniach bo Tobie wyszła inna
długość AC
Chociaż muszę mieć gdzieś błąd w obliczeniach bo Tobie wyszła inna
długość AC


 zauważyłem przy przepisywaniu
dopiero. W takim razie nie wiem gdzie jest błąd
zauważyłem przy przepisywaniu
dopiero. W takim razie nie wiem gdzie jest błąd
 Czas na następne zadanka 'tego typu'.
A tak nawiązując do tego zadania i innego, które robię, czy mógłbyś zobrazować na rysunki jakie
sa odcinki dokładnie w trapezie równoramiennym wpisanym w okrąg?
I drugie pytanko, jeśli mam trójkąt prostokątny i poprowadzę środkową od kąta prostego to
środkowa będzie równa połowie przeciwprostokątnej, prawda? Tam wyjdzie trójkąt
równoramienny...
Czas na następne zadanka 'tego typu'.
A tak nawiązując do tego zadania i innego, które robię, czy mógłbyś zobrazować na rysunki jakie
sa odcinki dokładnie w trapezie równoramiennym wpisanym w okrąg?
I drugie pytanko, jeśli mam trójkąt prostokątny i poprowadzę środkową od kąta prostego to
środkowa będzie równa połowie przeciwprostokątnej, prawda? Tam wyjdzie trójkąt
równoramienny...
 NIe za bardzo wiem, co co CI chodzi z tymi odcinkami w trapezie równoramiennym.
Co do trójkąta prostokątnego.
Środkowa to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
NIe za bardzo wiem, co co CI chodzi z tymi odcinkami w trapezie równoramiennym.
Co do trójkąta prostokątnego.
Środkowa to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.