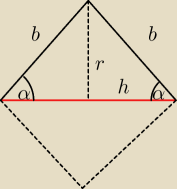
stereometria salamandra: Zadaie: Trójkąt równoramienny o obwodzie k obraca się wokół podstawy. Jakie powinny być długości boków tego trójkąta, aby objętość powstałej bryły była największa>? tutaj to już w ogóle nie wiem co od czego uzależnić, wyznaczyłem na razie tyle co mogłem, ale nie wiem czy to się przyda h=√b²−r² b=√r²+h²

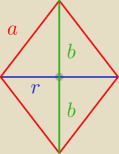
Saizou : 2a+2b=k a+b=k r=√a²−b²

	1		2
V=2*		*πr2*b=		*π*(a2−b2)*b
	3		3

i dalej sam

salamandra: zaraz zrobię, nie wydaje się jednak takie trudne, chyba w drugiej linijce masz błąd, powinno

	k
być
	2

i w zasadzie spytam− po co jest ten obwód, to "k", skoro nawet tego nie wykorzystamy?

Saizou : tak, powinno być

	k
a+b=
	2

tak to jest jak próbuje się dobrać "ładniejsze" zmienne

Saizou : korzystamy, trzeba go użyć aby zbudować funkcję jednej zmiennej, a nie dwóch tak jak podałem o 15:41

salamandra: 2h+2b=k

	k
h+b=
	2

r=√b²−h²

	2
V=		π*(b2h−h3), szczerze mówiac nie wiem jak użyć tego "k" w tym momencie
	3

nawet rozbicie na h(b²−h²)=h(b−h)(b+h) nie wiele mi daje

Jerzy:

	k
Masz dwie zmienne: h i b , a chcesz mieć jedną, np: b =		− h i wstawiasz do wzpru.
	2

salamandra:

	k
chyba, że b=		−h
	2

	k
t=
	2

f(h)=h(t−h−h)(t−h+h) f(h)=h(−2h+t)(t) f(h)=−2th²+t²h?

salamandra: o właśnie

Saizou : zauważ że masz V w zależności od dwóch zmiennych b oraz h, żeby się jednej pozbyć

	k		k
korzystamy z równości h+b=		→b=		−h , wówczas Jak wygląda V?
	2		2

+ założenia b>0 oraz h>0

k
	−h>0
2

	k
h<
	2

	k
h∊(0;		)
	2

salamandra:

	k		3k
Odp. h=		i b =		?
	8		8

Jerzy: Jeśli robisz podstawienie,to musisz zrobić założenia co do t

salamandra: f(h)=−2th²+t²h f'(h)=−4th+t² f'(h)=0 ⇔ −4th+t²=0 −4th=−t² / : (−4t)

	t
h=
	4

	k
t=
	2

	k
h=
	8

	k		k		4k		k		3k
b=		−		=		−		=
	2		8		8		8		8

Jerzy: Aj nie, u ciebie k/2 to stała, więc nic nie zakładasz o t.

salamandra: w przeciwnym wypadku t≠0 by wystarczyło?

Jerzy: Nieptrzebnie ci zamieszałem, k nie jest zmenną , więc t = k/2 jest nadal stałą.

salamandra: Nie dokończyłem, bo boki u mnie to przecież 2b i 2h, więc

	k
2h=
	4

	3k
2b=		,
	4

teraz dobrze?

Maturzysta : Hej, dlaczego we wzorze na V podstawiasz b² w miejscu, w miejsce promienia?

salamandra: r=√b²−h²

Maturzysta : V=²₃π(√b²−h²)² * √b²−h²? Dobrze myślę? Sorki za spam w twoim temacie, ale też ćwiczę optymalizację

salamandra:

	2
V=		π(√b2−h2)2*h
	3

Maturzysta : V(h) = ²₃π(¹₄k²h−kh²) Tak mi wyszło nie podstawiajac nic, jak pozbyles się π?

Maturzysta : Nie podstawiajac t*

salamandra:

2
	π pominąłem, bo nie ma ono w ogóle wpływu na miejsca zerowe pochodnej.
3

To tak jakbyś miał funkcję kwadratową: x²−3x−4 oraz 2(x²−3x−4) 1)x²−3x−4=0 Δ=9+16=25 x1=−1 x2=4 2)2x²−6x−8=0 Δ=36+64=100 x1=−1 x2=4

Saizou : zauważ, że f(h)=−2th²+t²h to funkcja kwadratowa i pochodna nie jest potrzebna

	1
h=		k
	8

	3
r=		k
	8

Maturzysta : Dzięki <3 Ostatecznie wyszło h=k/8, b=3k/8?

Saizou :

	3
nie r tylko b =		k
	8

salamandra: wiem Saizou, ale tak jakoś mi się pochodnej zachciało

Saizou : Na maturze trzeba czas szanować

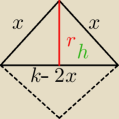
an: Czy nie łatwiej i szybciej: robimy rys. j/w jako x oznaczamy szukany bok, piszemy wzór na objętość bryły

	1
V=2*		πr2*h jak widać musimy znaleźć zależność r i h od x
	3

	k
2h=k−2x ⇒ h=		−x
	2

	k		k2
r2=x2−h2=x2−(		−x)2=kx−
	2		4

podstawiamy do wzoru

	1		2		k2		k		2		3		k3
V=2*		πr2*h=		π(kx−		)(		−x)=		π*(2kx2−		k2x+		)
	3		3		4		2		3		2		4

obliczamy pochodną

	2		3		k3		2		3
V'=		π*(2kx2−		k2x+		)'=		π*(4kx−		k2)
	3		2		4		3		2

przyrównujemy do zera i obliczamy ekstrema

2		3
	π*(4kx−		k2)=0
3		2

	3
x=		k
	8