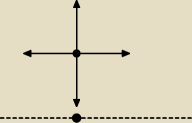
Jak opisać najkrótszą drogę równaniem? Cicada: Jak powinna poruszać się osoba z zasłoniętymi oczami będąca metr od celu aby przeszła najkrótszą drogę i trafiła do danego punktu ? Jak opisac to równaniem wykorzystując całki ?

wredulus_pospolitus: A możesz trochę bardziej wyjaśnić na czym ma polegać zadanie?

a7: no właśnie wyjaśnij trochę bardziej, czy jest jakiś sygnalizator właściwego kierunku czy jakieś "ciepło zimno" czy zupełnie na oślep, ("teoretycznie"(?) rzecz biorąc może mogłaby wystawić nogę na metr i zatoczyć okrąg)

wredulus_pospolitus: Albo poruszać się 'po ślimaku' z rozłożonymi na boki rękoma, aby zwiększyć szanse na 'padnięcie' na cel. Tyle że nie mamy bladego pojęcia jak wygląda sytuacja.

Cicada: Właściwie to nie mam innych danych, osoba ta wie, że jest metr czy załóżmy jedną jednostkę od drogi, ale nie wie w jakim kierunku się udać, ma tylko jedną szansę a musi pokonać jak najkrótszą drogę aby tam się dostać na pewno, nie może się jej nie udać. Myślałem o ruchu spiralnym, ale nie wiem jak to opisać i czy tym sposobem będzie najkrócej ale na pewno by trafiła.

wredulus_pospolitus: Co to znaczy: 'ma tylko jedną szansę'

wredulus_pospolitus: Ruch spiralny się nie powiedzie jeżeli ma trafić w JEDEN KONKRETNY PUNKT Bo wystarczy że trafi o 3 milimetry wcześniej na daną wysokość albo o 3 milimetry za późno, to 'nie trafi w cel' Może byś tak słowo w słowo przekazał/−a treść zadania

a7: czy możesz nakreślić bardziej sytuację tej osoby lub swoją czy to sytuacja z życia czy problem teoretyczny i na jaki przedmiot to nam łatwiej będzie myśleć odpowiednimi kategoriami

wredulus_pospolitus: I jeszcze dodatkowe pytanie −−− czy ta osoba wie ile to jest 1 metr

a7: jedna jednostka a jeden metr to może być duża różnica, bo człowiek jest zwykle powiedzmy mniejszy niż x metrów i jeszcze powiedz jak ta osoba się orientuje że jest już tak gdzie być powinna bo np. w przypadku z życia byłoby to inaczej niż na pustyni

jc: Trochę się idzie prosto, potem po okręgu, a potem znów prosto, czy jakoś tak. Jak wrócę za kilka godzin może podam dokładnie rozwiązanie.

wredulus_pospolitus: JC −−− pytanie czy idąc z zawiązanymi oczami będziemy wiedzieć jak iść 'po okręgu' Najbardziej optymalnie byłoby pójść metr w jednym kierunki, następnie o okręgu o promieniu 1 metra, wtedy droga przebywa będzie nie dłuższa niż (1 + 2π) metra. Tylko jak osoba z zawiązanymi oczami ma wiedzieć jak się trzymać takiej drogi ?!

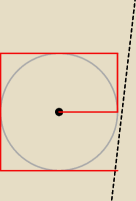
wredulus_pospolitus: Jeżeli osoba wie 'ile to jest 1 metr' (ilość kroków czy tam ile długości stóp −−− zapomniałem jak się na to mówiło w podstawówce), ale nie wie jak trzymać się wyznaczonego toru po okręgu, to wtedy taki tor będzie najbardziej optymalny, maksymalna długość to 8 metrów. Pod warunkiem, że osoba wie jak iść 'prosto', wykonanie skrętu pod kątem prostym jest banalne do zrobienia (wyciągamy rękę i obracamy tułów w jej kierunku tak aby była wyznaczała kierunek w którym podążamy.

wredulus_pospolitus: ale to jest już trafienie DO DROGI a nie do punktu.

wredulus_pospolitus: Może też (najprościej) poczekać aż coś przejedzie tą drogą −−− wtedy udać się w kierunku w którym odgłos przejeżdżającego samochodu był 'najgłośniejszy'

a7: ja bym jeszcze rozważyła pójście √2m w dowolną stronę powrót, obrót o 90 stopni i znowu √2m w zmienionym kierunku i powrót za czwartym razem maksymalnie powinno się udać

wredulus_pospolitus: Tu pewnie w grę wejdzie to: "ma tylko jedną szansę" −−− co ja interpretuję jako 'brak powrotu do miejsca startowego'. A nawet jeśli nie, to niestety: 7*√2 = 7*1.41 > 7 + 2.8 > 9

Kowal: A czy to zadanie to nie jest czasem https://en.wikipedia.org/wiki/Bellman%27s_lost_in_a_forest_problem ?

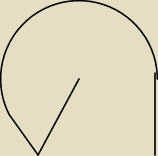
jc: Ten metr to trochę bez sensu, opis raczej dla mrówki. Idziemy √3/2 do przodu, skręcamy o 60 stopni w prawo i idziemy 1/2, potem idziemy po okręgu o promieniu 1 stycznym do ostatniego odcina (210^o), kończymy odcinkiem o długości 1.

jc: Wydaje mi się, że to coś takiego, ale nie pamiętam, jak uzasadnić, że lepiej nie można.

Cicada: @jc czy sam wymyśliłeś to rozwiązanie, czy na czymś się opierałeś/łaś?

wredulus_pospolitus: Ooo i się nagle Cicada pojawił/−a ... ale szczegółów zadania wcześniej napisać to nikt nie raczył. Pewnie to jakieś zadanie dodatkowe.

Cicada: Nie raczył, bo żadnych innych danych nie ma poza tymi, które wypisałEM.

jc: 5−6 lat temu dostałem to zadanie o kolegi. Nie pamiętam, jak znalazłem to rozwiązanie. Potem dowiedziałem się, ze takie samo rozwiązanie jest w jakimś zbiorze zadań. Nie próbowałem uzasadniać, że to najlepszy sposób.

wredulus_pospolitus: JC −−− na pewno zaczynam od √3/2 Wtedy nawet nie dojdziemy w linii prostej 'do drogi' A nasz 7/12 okręgu nie będzie miał tego samego środka co punkt startowy i wszystko się rozjedzie

jc: Narysuj sobie okrąg o promieniu 1 i o wiadomym środku. Koniec drogi możesz śmiało połączyć z dzióbkiem. Okrąg w całości mieści się w tak uzyskanej figurze.

wredulus_pospolitus: z punktu (0,0) idziemy do punktu (0, −√3/2) (czyli nie odwiedzamy punktu (0, − 1) ) idziemy pod kątem 60^o czyli po prostej y = −√3x/3 − √3/2 przez 1/2 jednostki czyli do punktu (−√3/4 , 1/4 − √3/2) odległość tego punktu od punktu wyjścia to o wiele mniej niż 1 jednostka czyli puki co nie mamy żadnej opcji wyłączonej i mieć nie będziemy więc nie lądujemy na okręgu o środku w (0,0) i promieniu 1. Więc ten fragment okręgu nie zawiera się w okręgu o środku w (0,0) i r = 1 ... więc opcje nie są wykluczane

wredulus_pospolitus: odległość tego punktu (od którego zaczynamy podróż po okręgu) od początku drogi (0,0) to trochę niespełna 0.753

	√4 − (3)1/2
(dokładniej to odległość ta wynosi		)
	2

wredulus_pospolitus:

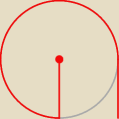
	√3
pierwszy odcinek musi być dłuższy niż		... musi być dłuższy niż 1, aby później móc
	2

pod kątem 60^o 'wejść na okrąg "styczności dróg" '. ale faktycznie można nie robić pełnego okręgu tylko taką drogę (2 + 3π/2) dzięki czemu schodzimy poniżej 7 jednostek długości

wredulus_pospolitus: jednak pod żadnym pozorem nie upieram się, że to co podałem to najkrótsza droga

jc: Ten pierwszy odcinek powinien mieć długość = 2/√3, a ten drugi 1/√3. Źle napisałem, ale rysunek pozostaje ten sam. Całość ma √3 + 1 + 7π/7 = 6.39... Na rysunku u Ciebie mamy 3π/2 + 2 = 6.71...

wredulus_pospolitus: jc −−− dlatego ja pisałem, że się nie upieram przy rozwiązaniu ... u Ciebie po prostu to √3/2 od początku mi jakoś nie pasowało

jc: Oj, zwyczajnie się pomyliłem, choć uczniowi zabrałbym połowę punktów za takie rachunki. Powyżej literówka, powinno być oczywiście 7/6 π.

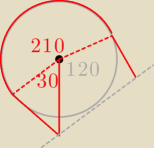
wredulus_pospolitus: Czyli droga miałaby wyglądać pi razy oko tak jak powyżej (tak wiem −−− odcinki nie są w skali) szczerze mówiąc ... nie mam siły tego liczyć ... wierzę na słowo

jc: Tak (mój rysunek wygląda bardziej realistycznie). Pisząc pierwszy list napisałem, co pamiętałem. Potem znalazłem rysunek bez opisu. Dopiero później zrozumiałem, dlaczego zaproponowana droga jest dobra (nie wiem, czy najlepsza, ale wydaje mi się, że mój kolega potwierdził kształt).

wredulus_pospolitus: Chociaż ... to nadal mi nie pasuje, ale nie mam siły liczyć tych pierwiastków Ja bym szybciej 'odrywał' się od okręgu (po przebyciu połowy okręgu) tak aby otrzymać prosta równoległą do drugiego odcinka i kończyć ją na stycznej do okręgu która przechodzi przez pierwszy punkt (nie wiem czy dobrze przelałem swoje przemyślenia)

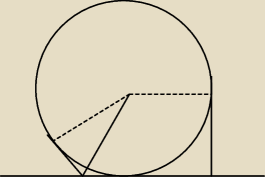
jc: Trójkąt ma kąty 30, 60, 90. Wysokość (linia przerywana) wynosi 1. Pozostałe boki 1/√3 i 2/√3.

wredulus_pospolitus: Ta ... masz rację ... no i z tej postaci widzę w jaki sposób wykazać najbardziej optymalne z tego typu rozwiązań