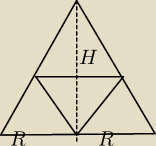
stereometria salamandra: Zadanie: W stozek o promieniu podstawy dlugosci R i wysokosci dlugosci H wpisano drugi stozek, którego wierzchołek leży w środku podstawy danego stozka. Okrąg ograniczajacy podstawę stozka wpisanego lezy na poweirzchni bocznej danego stożka. Wyznacz dlugość promienia podstawy stożka wpisanego przy której ma on największą objętość. dobry rysunek przekroju?

a@b: dobry

salamandra: dzięki, opłaca się w ogóle tworzącą wyznaczać jakoś za pomocą H i R i później ją jakoś wykorzystać czy jest to zbędne tutaj?

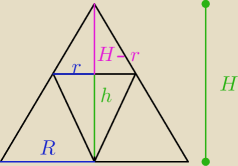
Saizou : Opłaca się I podobieństwo

salamandra: dzięki, zaraz spróbuję

Saizou :

	2
Jak się gdzieś nie machnąłem wychodzi odpowiedź r=		R
	3

salamandra: A ten odcinek fioletowy to czemu jest H−r?

Jerzy: Przez pomyłkę.

salamandra: Powinno być H−h, racja?

Jerzy:

salamandra: dzięki

Saizou : Jasne, że H − h, to moja nieuwaga

salamandra: Nie wiem co mam ze sobą przyrównać, chciałem

H		H−h
	=		, ale to mi nic nie da bo nadal bede mial r i h
R		r

wyznaczyłem też tworzącą: H²+R²=l² l=√H²+R²

Saizou : No tak, ale masz napisać funkcję objętości, czyli z proporcji

H		H−h
	=		możesz wyznaczy jedną zmienną w zależności od drugiej.
R		r

W ten sposób funkcję dwóch zmiennych V(r, h) "zredukujemy" do jednej zmiennej

salamandra: no ok, załóżmy mam

H		H−h
	=
R		r

Hr=RH−Rh

	RH−Rh
r=
	H

i z tego samego wyznaczyć jeszcze "h"?

Saizou : nie, bo się zakręcisz jak wyznaczysz h.

	1
V(r, h)=		*πr2*h
	3

i teraz musisz coś podstawić do tego wzoru, wówczas otrzymasz funkcję jednej zmiennej, której potrafisz obliczyć wartość największą

salamandra:

	RH−Rh
nie bardzo rozumiem czyli mam wstawić za "r", to wyliczone przeze mnie		? ale z
	H

tego nie ma prawa raczej wyjść

Jerzy: Dlaczego nie ma prawa ? Dostaniesz funkcję jednej zmiennej.

Jerzy: Równie dobrze mozesz policzyć h i podstawić do wzoru.

Saizou : polecam wyznaczyć h, bo masz znaleźć r, dla którego objętość stożka wpisanego będzie największa. To takie zadanie z optymalizacji. Zazwyczaj jest do znalezienia jakaś zależność, którą wykorzystuje się w funkcji maksymalizującej (minimalizującej). Np. Dany jest prostokąta o obwodzie równym 20. Znajdź prostokąt, którego pole jest największe. Nasza zależność, to 2a+2b=20 →a=10−b a funkcje maksymalizująca to P(a,b)=ab P(b)=b(10−b)

salamandra:

1		R2H2−2R2Hh+R2h2
	*π*		*h, wlaśnie dlatego według mnie nie ma prawa, nie wiem co
3		H2

dalej z takim czymś

Saizou : R, H to nasze dane, je traktujesz jako liczby.

Jerzy:

	π
Wyłacz		, licznik wymnóż przez h i licz maksimum.
	3H2

salamandra: cyzli co, mogę wstawić dowolną liczbę?

Saizou : Nie, chodzi o to, że jak będziesz liczyć pochodną, to traktujesz to jako liczby.

Jerzy: Traktujesz jako stałą. Np: f(h) = 4Hh² , to f'(h) = 4H*2h = 8Hh

salamandra:

	π
f(h)=		*(R2h3−2R2H*h2+R2H2*h)
	3H2

f'(h) = 3R²h²−4R²Hh+R²H² o to chodziło Jerzy?

Jerzy: (R²H²*h − 2R²Hh² + R²h³)' = R²H² −4R²Hh + 3R²h²

Jerzy:

salamandra: f'(h)=3R²h²−4R²Hh+R²H² Δ=16R⁴H²−12R²*R²H²=16R⁴−H²−12R⁴H²=4R⁴H² √Δ=2R²H

	4R2H−2R2H		12R2H		H
h1=		=		=
	6R2		6R2		3

	4R2H+2R2H
h2=		=H
	6R2

	H
maksimum dla h1, więc h=
	3

i co teraz o ile to jest dobrze?

Jerzy: No oczywiście to co napisałeś , to tylko pochodna nawiasu , a przed nim musi być stała, bo: f'[a*f(x)] = a*f'(x)

salamandra:

	H   RH−R*   3		RH   RH−   3		R		2
ok, wstawiłem do r=		=		= R−		=		R
	H		H		3		3

salamandra: chyba w tym wypadku tę stałą mogę pominąć prawda? bo nie liczę konkretnej wartości?

Jerzy: Tak. Interesują cię miejsca zerowe pochodnej, czyli miejsca zerowe nawiasu. Dla a ≠ 0 , a*x = 0 ⇔ x = 0

salamandra: dzięki.... troche zagmatwane to zadanie dla mnie było... nie rozumiem tego, że tu coś traktujemy jako stałą, tu coś tam wyznaczamy w zależności od tamtego, jeżeli wszystkie optymalizacyjne zadania ze stereometrii są takie, to krzyż na drogę dla mnie

Saizou : Dasz radę, policzysz kilka takich zadań i będzie z górki

Jerzy: Jeśli w treści zadania masz powiedziane ,że wysokość to H , to traktujesz to jako pewną stałą, której wartość nas nie interesuje Rozwiąż przykład z 14:49 od Saizou.

salamandra: Jerzy, akurat takie zadania jak podał Saizou miałem miesiąc temu przy okazji planimetrii i one były znośne, a tutaj to czarna magia, przynajmniej z początku

Jerzy: Mechanizm jest zawsze ten sam w przypadku zadań optymalizacyjnych.

salamandra: Dostaje czkawki, gdy nie ma żadnych liczb, tylko same literki, tak jak w przypadku zadania, które przed chwilą wstawiłem− z tydzien temu wrzucałem tu zadanie niemalże identyczne, tylko obwód był podany, oraz jakiś tam kąt i co prawda trzeba bylo konkretną objętość obliczyć, ale tam wiedziałem jak ruszyć przynajmniej

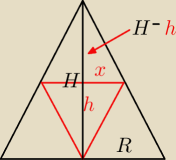
an: Jak poprzednio Ci napisałem zobacz jak proste jest to zadanie algebrę przecież miałeś to skąd ta rozpacz nad paroma literkami

	1
V=		πx2h wyznaczamy zależność h od x , np. z proporcji
	3

H		H−h		H
	=		⇒h=		(R−x)
R		x		R

	1		1		H		H
V=		πx2h=		πx2		(R−x)=		π(Rx2−x3)
	3		3		R		3R

	H		H
V'=(		π(Rx2−x3))'=		π(2Rx−3x2)
	3R		3R

H
	π(2Rx−3x2)=0
3R

x(2R−3x)=0

	2
x=0 lub x =		R
	3

salamandra: Dziękuję Ci, masz rację, tylko po prostu trzeba wiedzieć co od czego uzależnić, co wziąć za stałą itp i z tym miałem/mam problem.