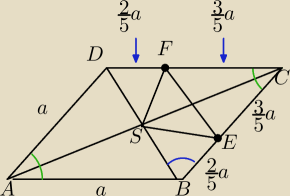
rombie ABCD przekątne przecinają się w punkcie S Anna: W rombie ABCD przekątne przecinają się w punkcie S oraz |AB| = a, |∡BAD| = α, α ∊ (0,π/2). Na boku BC i CD wybrano punkty E i F tak, że |BE| : |EC| = |DF| : |FC| = 2 : 3. Oblicz pole trójkąta EFS

a7: liczymy pole rombu z wzoru z sinusem kąta α P=a²sinα PΔEFS=P−PΔEFC−(1/2)*P−2*PΔBES PΔBES liczymy z wzoru z sinusami, a przedtem z tw. cosinusów liczymy odcinek BS

	DB
np.BS=		=d/2
	2

d²=a²+a²−2a²cosα=2a²(1−cosα) |BS|=a√(1−cosα) PΔBSE=1/2*2/5a*a√(1−cosα)*cos(90−α/2)=.... PΔEFS=P−PΔEFC−(1/2)*P−2*PΔBES niestety nie działa robienie rysunków

a7: PΔEFC=1/2*3/5a*3/5a*sinα

a7: wychodzi mi PΔEFS=2/5a²*(4/5sinα−√1−cosα*cos(90−α/2))

a7:

a@b: 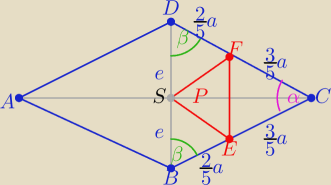P(EFS)= P(BCD)−2P(BSE)−P(ECF) i e=a*sin(α/2) i sinβ= cos(α/2) oraz 2sin(α/2)*cos(α/2)= sinα zatem

	a2		1		2		1		3
P=		sinα −2*		*e*		a*sinβ−		*(		a)2*sinα
	2		2		5		2		5

	a2		2a2		9a2
P=		sinα −		*cos(α/2)*sin(α/2) −		sinα
	2		5		50

P=.......

	3a2sinα
P=
	25

================