pomoc zadniu z okregu
jaros: Wyznacz równanie okręgu stycznego do obu osi układu współrzędnych i do okręgu o równaniu
x
2 + y^2 – 34x – 28y + 385 = 0. Rozpatrz wszystkie przypadki. Srodek okregu i promien to x=17
y=14 r=10
Widze z rysunku ze jeden okrag bedzie mial współrzędne (5,5) oraz r=5 ale jak to wgl obliczyć

2 mar 22:21
salamandra: Ten środek i promień był podany w zadaniu?
2 mar 22:22
salamandra: a rozumiem, to sie tyczy tego okręgu podanego.
2 mar 22:23
jaros: Nie nie wysztko wyliczyłem z rówania okregu a jeden okrag zauwazylem z rysunku lecz w matmie
trzeba wszystko wyliczyć
2 mar 22:25
salamandra: Pierwszy przypadek− styczne wewnętrznie, drugi przypadek− styczne zewnętrznie zapewne.
2 mar 22:25
jaros: No si ale jak je wyznaczyc
2 mar 22:29
salamandra: chociaż styczne wewnętrznie już można odrzucić, bo skoro S(17,14) i r=10, to ten okrąg będzie w
pierwszej ćwiartce i nie będzie stykał się z osiami
2 mar 22:29
jc: Wydaje się, że będziemy mieli 4 takie okręgi.
2 mar 22:30
jaros: Robiłem podobne zadania ale miałem podany punkt i trzbea bylo wyliczyc rówania okregów styczne
do niego ale nigdy nie robilem takiego zadania i nie mam pojecia o co tu chodzi
2 mar 22:30
jc: (a−r)2+(b−r)2=(R+r)2 lub (a−r)2+(b−r)2=(R−r)2, R=17, a=17, b=14
r szukany promień
2 mar 22:34
jc: R=10
r2−2(R+a+b)r+a2+b2−R2=0
r2−82r+385=0
r=5 lub r=36
Zostaje drugi przypadek.
2 mar 22:38
jaros: r2−2(R+a+b)r+a2+b2−R2=0 co to za rówanie?
2 mar 22:41
jaros: a to już nie są dwa przypadki?
2 mar 22:42
jc: r2−42r+385=0
Tu już nie jest tak ładnie lub coś pomyliłem.
r=21+2√14 lub r=21−2√14.
2 mar 22:42
jaros: mam tak samo wynik z 2
2 mar 22:47
jc: Razem mamy 4 przypadki. Okręgi styczne zewnętrznie (2 rozwiązania) i okręgi styczne
wewnętrznie (też 2 rozwiązania).
Co do równania, uważam, że czasem lepiej panuje się nad szczegółami, kiedy napisze się równanie
z parametrami, a nie konkretnymi liczbami.
Szukany okrąg ma promień r i środek w punkcie (r,r).
Kwadrat odległości (r,r) od (a,b) = (a−r)2 + (b−r)2.
Kiedy okręgi są styczne to odległość pomiędzy środkami jest sumą lub różnicą promieni.
2 mar 22:47
jaros: ale cholera odpowiedzi bede mial dopiero w czwartek
2 mar 22:47
salamandra: Jesteś pewien, że będą styczne wewnętrznie, jeśli dany okrąg leży w pierwszej ćwiartce i nie
styka się z osiami, a ten szukany okrąg ma być styczny do osi? Chyba, że istnieje możliwość,
że to ten dany okrąg będzie "wewnątrz" tego szukanego?
2 mar 22:48
2 mar 22:53
jc:
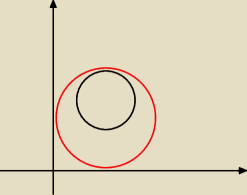
Pozostałych 3 nie narysowałem.
2 mar 22:54
jc: Promień drugiego = 77. 385=5*77.
2 mar 22:56
jaros: Promienie 77 i 5 pasuja

2 mar 23:02
jaros: Ale jak wyliczyles 77?
2 mar 23:02
jc: Drugi pierwiastek równania kwadratowego. Za pierwszym razem coś pomyliłem
Jeszcze trzeba poprawić drugi przypadek.
2 mar 23:09
jaros: nie rozumiem o co tu wgl chodzi

2 mar 23:16
jc: Pozostałe 2 pierwiastki są dobrze policzone.
2 mar 23:17
jc: a=17, b=14, R=10
Masz dwa równania, które dają Ci 4 promienie szukanego okręgu.
(r−a)2+(r−b)2=(R+r)2, okręgi styczne zewnętrznie,
(r−a)2+(r−b)2=(R−r)2, okręgi styczne wewnętrznie,
Równanie szukanego okręgu
(x−r)2+(y−r)2=r2.
2 mar 23:21
jaros: no ale r=21+2√14 lub r=21−2√14. nie pasuja
2 mar 23:25
jaros: dobra jednak wszystko sie zgadza
2 mar 23:28

 Pozostałych 3 nie narysowałem.
Pozostałych 3 nie narysowałem.

