stereometria salamandra: Zadanie: Kulę metalową o promieniu R przetopiono na stożek, którego pole powierzchni bocznej jest trzy razy większe od pola jego podstawy. Oblicz długość wysokości i promienia podstawy stożka. Wykonaj obliczenia dla R=³√2 No i nie wiem jak to zrobić, bo wydawało mi się, że ten promień kuli to będzie również promień podstawy stożka, ale chyba nie. Bo ja zrobiłem tak Pp=π*(³√2)²= ³√4π Pb=3*³√4π Pb=πRl 3³√4π=π*³√2*l / : π 3³√4=³√2*l l=3³√2

a7: trzeba obliczyć objętość kuli i tą samą objętość ma stożek, ale nie promień podstawy

salamandra: Jak to może mieć tę samą objętość, gdy części kuli się pozbędziemy, czy źle myślę?

a7: V_Kuli=4/3π*2=8/3π 3πr²=πrl r=l/3 H=P{l²−(l²/9)} H=(2l√2)/3

	l		2l√2
VS=1/3π		*
	3		3

	l		2l√2
8/3π=1/3π(		)2*
	3		3

a7: kulę przerobiono na stożek czyli rozumiem, że stopiono całą i zrobiono z niej stożek ( z tego metalu z którego była)

salamandra: Rozumiem teraz, ja to myślałem, że tak jakby zostalo troche materiału straconego i powstał stożek zrobiłem tak:

4		1
	π*(3√2)3=		PpH
3		3

4		1
	π*2=		*Pp*H
3		3

8		1
	π=		*Pp*H
3		3

2) Pp=πr² gdzie r= promien stozka Pb=πrl gdzie l= tworząca stozka Pb=3πr² (bo trzykrotność pola podstawy) πrl=3πr²

	3πr2
l=		= 3r
	πr

3) z tw. Pitagorasa (promień, wysokość, tworząca) H²+r²=(3r)² H²+r²=9r² H²=8r² H=2r√2 4) mając jedną niewiadomą wstawiam do objętości kuli

8		1
	π=		*πr2*2r√2
3		3

8		1
	=		*2r3√2 / * √2
3		3

8√2		1
	=		*2r3*2
3		3

8√2		4
	=		r3 / * 3
3		3

8√2= 4r³ 2√2=r³

	1		1
8(		) (do potęgi		) = r3
	2		2

	1		1
8(		) (do potęgi		) = r
	6		6

⁶√8= ⁶√2³ = √2 H=8r² = 8*2=16 Domyślam się że w czwartym punkcie można to było jakoś łatwiej zrobić?

Mila:

	4πR3
Vk=
	3

	1
Vs=		π r2*h
	3

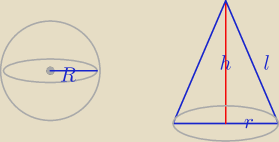
============ 1)3πr²=π*r*l z treści zad. l=3r h²=(3r)²−r² h=√8*r

	4πR3		1
2)		=		*π*r2*√8*r −porównanie objętości
	3		3

licz dalej sam, chcę widzieć, jak sobie poradzisz z pierwiastkami i potęgami

Mila: cd. 4*2=√8=r³

23
	=r3
√23

	2
r=
	√2

r=√2

salamandra: No to wyszło , dziękuję