trygonometria
123321: Jak określić dziedzinę i zbiór wartości tej funkcji?
| | 1+sin2 x− cos2 x | |
f(x)= |
| |
| | sin2 x − sin4 x | |
| | 2 | |
przekształciłam to do postaci: f(x)= |
| |
| | cos2 x | |
ale co z dziedziną i zbiorem?
2 mar 13:44
Jerzy:
A jak to przekształciłeś ?
2 mar 13:46
Jerzy:
A dobra , nie zauważyłem,że tam jest sin4x.
Zacznij od dziedziny: cos2x ≠ 0
2 mar 13:47
Saizou :
Jerzy jak tak zrobimy to stracimy wyrzucenie z dziedziny sinx ≠ 0
Najpierw dziedzina potem przekształcenia.
sin2x−sin4x≠0
sin2x(1−sin2x)≠0
sin2x≠0 1−sin2x≠0
sinx≠0 cos2x≠0
cosx≠0
2 mar 13:49
a7:
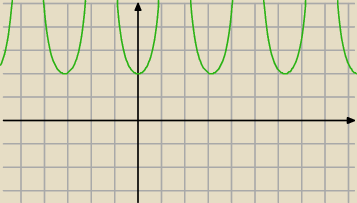
2 mar 13:50
Saizou :
a7 z rysunku jaki zbiór wartości byś odczytał?
2 mar 13:52
Jerzy:
Racja
Saizou ,a sam przestrzegam przed przekstałcaniem wzorów przed ustaleniem dziedziny

2 mar 13:53
a7:
<2,+∞)
2 mar 13:54
Saizou :
a7 to źle bo przedział (2; +∞), z tego powodu, że wyrzucamy x = kπ, czyli przypadek
gdy sinx=0
2 mar 13:55
Jerzy:
| | 2 | |
Zbiór wartości funkcji liczysz z postaci: f(x) = |
| |
| | cos2x | |
Maksymalna wartośc mianownika to 1 , stąd f
min = 2
Grnica f(x)
x→ =
∞ . czyli: Z
f = [2,
∞)
2 mar 13:57
2 mar 13:58
Jerzy:
Nie masz racji Saizou , fmin =2
2 mar 14:02
Jerzy:
A jednak nie, masz rację. Zapomniałem o sinusie

2 mar 14:04
Saizou :
z drugiej strony jeśli maksymalna wartość mianownika wynosi 1 i jest ona osiągana dla x=2kπ
ale wartości kπ usuwamy z dziedziny, bo sinx≠0.
Gdzieś tutaj jest jakiś zgrzyt.
2 mar 14:06


