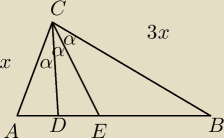
Oblicz stosunek: CD do CE
To było zadanie wykaz ze to jest
ileś tam cosinusów kwadrat coś tam przez
cosinus no ale nie ważne. W ogóle nie wiem za co się zabrać
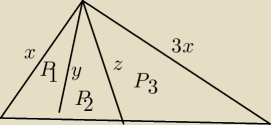
| 3xsin3α | ||
P1=(1/2)*xysinα P1=P−(1/2)*y*3xsin2α przyrównujemy i mamy y= | ||
| sinα+3sin2α |
| 3xsin3α | ||
P3=(1/2)*3xzsinα P3=P−(P1+P2)=1/23x2sin3α−1/2xzsin2α z= | ||
| 3sinα+sin2α |
| y | sin2α+3sinα | ||
= | |||
| z | sinα+3sin2α |
| y | 2sinαcosα+3sinα | 2cosx+3 | |||
= | ={sinα(2cosα+3)}{sinα(1+6cosα)}= | ||||
| z | sinα+3*2sinαcosα | 1+6cosα |
!