Stereometria
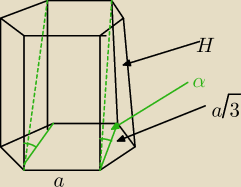
garbatek: Graniastosłup prawidłowy sześciokątny przecięto płaszczyzną przechodzącą przez dolną i górną
krawędź podstawy, które nie należą do tej samej ściany bocznej. Pole powierzchni otrzymanego
przekroju jest równe 26 √2 , a przekątna ściany bocznej graniastosłupa tworzy z płaszczyzną
podstawy kąt o mierze tan(a)=√61
ma ktoś pomysl jak to zrobic? .
2 mar 01:12
a7: a co trzeba policzyć?
2 mar 01:58
garbatek: Oblicz długość krawędzi podstawy tego graniastosłupa.
2 mar 02:00
a7: no spoko biorę się za to
2 mar 02:00
2 mar 02:10
a7:
tgα=H/(a
√3)
H=
√61a
√3=a
√183
d
2=H
2+a
2
d=a
√184=2a
√46
26
√2=a*d
26
√2=2a
2√46
trochę dziwny wynik
2 mar 02:10
a7: a jest prawidłowy wynik?
2 mar 02:11
garbatek: nie mam wyników
2 mar 02:26
garbatek: jeszcze objetosc musze policzyc
2 mar 02:36
2 mar 02:42
garbatek: inne a?
2 mar 02:43
a7: tak, ale warte chyba tyle samo gdyż tylko skróciłam dwójkę z pierwiastka z dwóch przez 46 z
pierwiastka z 46
2 mar 02:44
garbatek: minimalnie inny wynik jest o pare dziesiętnych
2 mar 02:45
garbatek: a jaki dokładny wynik po przecinku objetosci?
2 mar 02:45
a7: V mi wychodzi takie, że wolę nie wpisywać
2 mar 02:45
a7: 157,42.....
2 mar 02:46
garbatek: takie wlasnie w tych zadaniach wychodzą bo dane sa generowane losowo
2 mar 02:46
a7: ale gdzie jest ten minimalnie inny wynik (bo nie zajrzałam do Twojego linku)
2 mar 02:46
2 mar 02:48
a7: ?
2 mar 02:48
a7: V=39
32*23
−34*183
12*2
−1
2 mar 02:57
a7: jednak wątpię aby to był prawidłowy wynik ?
2 mar 02:58
Bogdan:
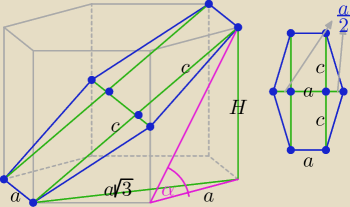
H = a*
√61, 2c =
√ 61a2 + 3a2 = 8a
2 mar 10:24
a7: elegancko!
2 mar 15:53