Stereometria
KamilS1: W prostopadłościanie ABCDA'B'C'D punkty P Q R są środkami krawędzi, odpowiednio AB CC' i A'D'
Wyznacz najkrótszy bok trójkąta PQR
|AB|=48
|BC|=32
|CC'|=84
Bardzo prosze o pomoc mam 20 minut aby oddac to zadanie
2 mar 00:54
wredulus_pospolitus:
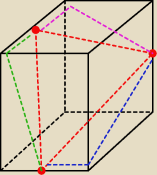
kolorami zaznaczyłem z jakich trójkątów prostokątnych (przyprostokątnych) możesz skorzystać w
celi wyznaczenia długości boków tego trójkąta PQR
2 mar 01:07
a7:
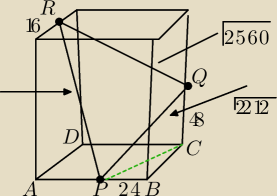
RP jest najdluższa?
PQ najkrótsza równa
√2212 
(2 razy Pitagoras)
2 mar 01:15
wredulus_pospolitus: no i czas minął

2 mar 01:19
wredulus_pospolitus:
dziwny deadline −−− 01:14

2 mar 01:19
a7: może dosyłka internetowa na jakąś zalkę
2 mar 01:31
wredulus_pospolitus:
Zapewne ... ale nadal − dziwna godzina na deadline
to już by była jakaś pełna godzina (do północy chociażby)
2 mar 01:32
a7: hmm
2 mar 01:56
Wojtek: wyszły mi inne liczby z tego pitagorasa (58, 2√1081 i 4√493) i na końcu muszę podać sinus
kąta PQR i z twierdzenia cosinusów chcialem wyciagnac ale kosmiczne liczby wychodzą.
2 mar 01:59
a7: no a zdążyłeś w ogóle?

2 mar 02:15
a7: ja niestety mylę się nieraz w pierwszych obliczeniach
2 mar 02:16
wredulus_pospolitus:
|AB| = 48 = 3*42
|BC| = 32 = 2*42
|CC'| = 84 = 21*4
|PQ| = √242 + 422 + 322 = √3364 = 58
|QR| = √482 + 422 + 162 = 2√1081
|RP| = √242 + 842 + 162 = 4√493
2 mar 02:24
wredulus_pospolitus:
7'888 = 3364 + 4324 − 232
√1081*cosα
α jest niemalże kątem prostym
2 mar 02:32
Mila:
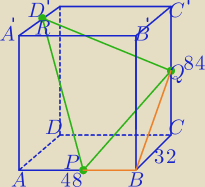
PQ− najkrótszy bok ΔPQR
|PQ|
2=24
2+32
2+42
2
|PQ|=58
Z ciekawości to liczyłam

Pozdrawiam rozwiązujących.
2 mar 15:25
a7: Pozdrawiam

2 mar 15:28
 kolorami zaznaczyłem z jakich trójkątów prostokątnych (przyprostokątnych) możesz skorzystać w
celi wyznaczenia długości boków tego trójkąta PQR
kolorami zaznaczyłem z jakich trójkątów prostokątnych (przyprostokątnych) możesz skorzystać w
celi wyznaczenia długości boków tego trójkąta PQR
 RP jest najdluższa?
PQ najkrótsza równa √2212
RP jest najdluższa?
PQ najkrótsza równa √2212  (2 razy Pitagoras)
(2 razy Pitagoras)



 PQ− najkrótszy bok ΔPQR
|PQ|2=242+322+422
|PQ|=58
Z ciekawości to liczyłam
PQ− najkrótszy bok ΔPQR
|PQ|2=242+322+422
|PQ|=58
Z ciekawości to liczyłam Pozdrawiam rozwiązujących.
Pozdrawiam rozwiązujących.
