wyznacznie funkcji Lolek: W ostrosłupie prawidłowym czworokątnym odległość środka podstawy ostrosłupa od jego krawędzi bocznej wynosi √3. a) Wyznacz objętość V ostrosłupa jako funkcję jego wysokości x i podaj dziedzinę tej funkcji b) Dla jakiej wartości x objętość ostrosłupa jest najmniejsza? Oblicz tę objętość. c) Naszkicuj wykres funkcji V Bardzo proszę o pomoc i z góry dziękuję

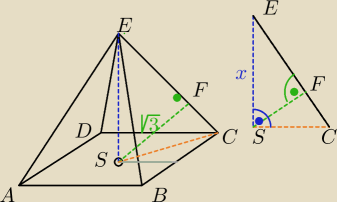
ite: |EF|²=x²−3

	|EF|		√3
ΔEFS∼ΔSFC →		=
	x		|SC|

√x2−3		√3
	=
x		|SC|

Jeśli wyliczysz z tej proporcji |SC|, to możesz wyliczyć pole podstawy i objętość w zależności od x czyli pkt a/

a7:

	a√2
|SC|=
	2

a√2		√3x
	=
2		√x2−3

	x√6
a=
	√x2−3

	1
V=		*a2*x
	3

	1	6x2
V(x)=			*x
	3	x2−3

	2x3
V(x)=
	x2−3

?

a7:

a7: ?

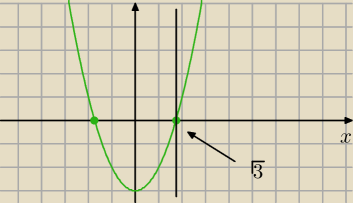
a7: Dziedzina x>0 x²−3>0 (x−√3(x+√3)=0 D: x∊(√3,∞) (?)

a7: tutaj prawidłowy wykres https://www.wolframalpha.com/input/?i=y%3D%282x%5E3%29%2F%28x%5E2-3%29

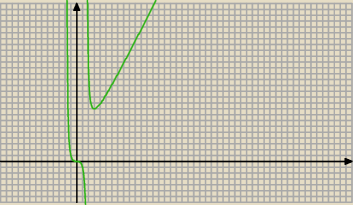
a7: V(x)_min=9 dla x=3

a7: V(x)_min=9 dla x=3 , żeby to wyliczyć trzeba policzyć pochodną i minimum lokalne czyli przyrównać pochodną do zera

	6x2(x2−3)−2x3*2x
V'(x)=
	(x2−3)2

2x2(x2−9)
	=0 ⇔ (x2−9)=0 czyli x=3 lub x=−3 sprzeczne
(x2−3)2

	2*33		54
dla x=3 Vmin(x)=		=		=9
	32−3		6

wyszło

Lolek: Super ,dziękuję bardzo