 Proszę o potwierdzenie rozwiązania zadań, będę je po kolei dodawał:
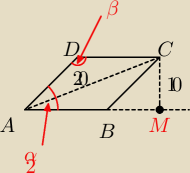
1. Podstawą graniastosłupa prostego jest romb przedstawiony na rysunku. Ściany boczne tego
graniastosłupa tworzą kąty dwuścienne o miarach:
Rozważam trójkąt ACM.
z tw. sinusów:
Proszę o potwierdzenie rozwiązania zadań, będę je po kolei dodawał:
1. Podstawą graniastosłupa prostego jest romb przedstawiony na rysunku. Ściany boczne tego
graniastosłupa tworzą kąty dwuścienne o miarach:
Rozważam trójkąt ACM.
z tw. sinusów:
| 20 | 10 | |||||||||||
= | ||||||||||||
| sin90 |
|
| α | ||
10=20*sin | ||
| 2 |
| α | 1 | |||
sin | = | |||
| 2 | 2 |
| α | |
=30 | |
| 2 |
| α | 10 | 1 | ||||
sin | = | = | ||||
| 2 | 20 | 2 |
| α | |
=30 czyli α=60 czyli β=120 | |
| 2 |
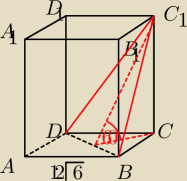 2. Trójkąt DBC1 jest przekrojem graniastosłupa prawidłowego czworokątnego, który tworzy z
płaszczyzną podstawy kąt 60. Wysokość tego graniastosłupa ma dlugosc:
DB=12√6*√2 = 12√12=24√3
2. Trójkąt DBC1 jest przekrojem graniastosłupa prawidłowego czworokątnego, który tworzy z
płaszczyzną podstawy kąt 60. Wysokość tego graniastosłupa ma dlugosc:
DB=12√6*√2 = 12√12=24√3
| H | ||
tg60= | ||
| 12√3 |
| H | ||
√3= | ||
| 12√3 |

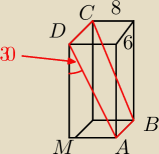 3. Czworokąt ABCD jest przekorjem prostopadłościanu przedstawionego na rysunku. Pole tego
przekroju jest równe
Rozważam trójkąt AMD
3. Czworokąt ABCD jest przekorjem prostopadłościanu przedstawionego na rysunku. Pole tego
przekroju jest równe
Rozważam trójkąt AMD
| 8 | ||
sin30= | ||
| AD |
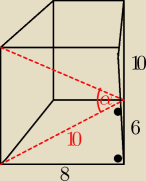 4. W podstawie graniastosłupa prostego jest trapez prostokątny którego kąt ostry ma miarę 36
stopni. Największy kąt dwuścienny jaki tworzą ściany tego graniastosłupa ma miarę równą:
144 stopnie, tu nie wymaga chyba obliczeń, chyba że jest to podchwytliwe.
5. Podstawą graniastosłupa prostego jest trapez prostokątny. Najdłuższa przekątna tego
graniastosłupa tworzy z płaszczyzną kąt?
4. W podstawie graniastosłupa prostego jest trapez prostokątny którego kąt ostry ma miarę 36
stopni. Największy kąt dwuścienny jaki tworzą ściany tego graniastosłupa ma miarę równą:
144 stopnie, tu nie wymaga chyba obliczeń, chyba że jest to podchwytliwe.
5. Podstawą graniastosłupa prostego jest trapez prostokątny. Najdłuższa przekątna tego
graniastosłupa tworzy z płaszczyzną kąt?
| 10 | ||
tgα= | ⇔ α=45 | |
| 10 |
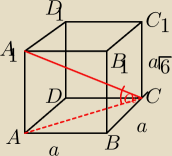 6. Kąt jaki tworzy przekątna graniastosłupa prawidłowego czworokątnego z płaszczyzną podstawy
ma miarę równą?
AC=a√2
6. Kąt jaki tworzy przekątna graniastosłupa prawidłowego czworokątnego z płaszczyzną podstawy
ma miarę równą?
AC=a√2
| a√2 | √2 | √12 | 2√3 | |||||
tgα= | = | = | = | = √3 | ||||
| a√6 | √6 | 2 | 2 |
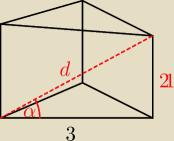 7. Krawędź boczna graniastosłupa prawidłowego trójkątnego jest 7 razy dłuższa od krawędzi
podstawy. Cosinus kąta jaki tworzy przekątna ściany bocznej z płaszczyzną podstawy jest równy.
212+32=d2
d2=450
d=√450 = 3√50=15√2
7. Krawędź boczna graniastosłupa prawidłowego trójkątnego jest 7 razy dłuższa od krawędzi
podstawy. Cosinus kąta jaki tworzy przekątna ściany bocznej z płaszczyzną podstawy jest równy.
212+32=d2
d2=450
d=√450 = 3√50=15√2
| 3 | 3√2 | √2 | ||||
cosα= | = | = | ||||
| 15√2 | 30 | 10 |
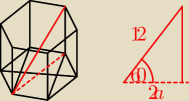 8. Najdłuższa przekątna graniastosłupa prawidłowego sześciokątnego ma długość 12 i tworzy z
najdłuższą przekątną podstawy kąt o mierze 60. Zatem krawędź podstawy tego graniastosłupa ma
dlugosc:
8. Najdłuższa przekątna graniastosłupa prawidłowego sześciokątnego ma długość 12 i tworzy z
najdłuższą przekątną podstawy kąt o mierze 60. Zatem krawędź podstawy tego graniastosłupa ma
dlugosc:
| 2a | ||
cos60= | ||
| 12 |
| 1 | 2a | ||
= | |||
| 2 | 12 |
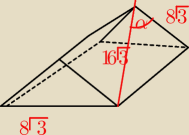 9. W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z krawędzią
podstawy kąt o mierze równej:
9. W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z krawędzią
podstawy kąt o mierze równej:
| 8√3 | 1 | |||
cosα= | = | |||
| 16√3 | 2 |
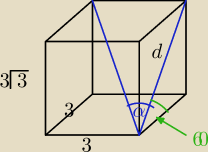 10. Przekątna graniastosłupa prawidłowego czworokątnego tworzy z przekątną ściany bocznej kąt
α. Zatem tgα=?
10. Przekątna graniastosłupa prawidłowego czworokątnego tworzy z przekątną ściany bocznej kąt
α. Zatem tgα=?
| 3 | ||
cos60= | ||
| d |
| 3 | 1 | |||
tgα= | = | |||
| 6 | 2 |
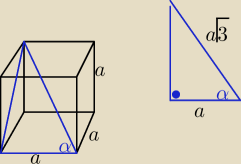 Prawda/Fałsz
Prawda/Fałsz
| √3 | ||
W sześcianie przekątna tworzy z krawędzią podstawy taki kąt α, że cosα= | ||
| 3 |
| a | 1 | √3 | ||||
cosα= | = | = | ||||
| a√3 | √3 | 3 |
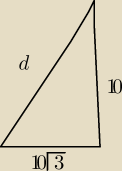 Prawda/Fałsz
W graniastosłupie prawidłowym sześciokątnym, którego wszystkie krawędzie mają dlugosc 10,
krótsza przekątna ma długość równą 20?
10√3, bo przekątna podstawy (krótsza) to dwie wysokości trójkąta równobocznego o boku 10.
102+(10√3)2=d2
d=√400=20
Prawda
Prawda/Fałsz
W graniastosłupie prawidłowym sześciokątnym, którego wszystkie krawędzie mają dlugosc 10,
krótsza przekątna ma długość równą 20?
10√3, bo przekątna podstawy (krótsza) to dwie wysokości trójkąta równobocznego o boku 10.
102+(10√3)2=d2
d=√400=20
Prawda
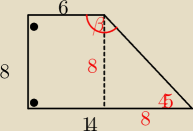 Prawda/Fałsz
W podstawie graniastosłupa prostego jest trapez prostokątny. Największy kąt dwuścienny tego
graniastosupa ma miare rowna 150?
Więc największy kąt= 135, więc fałsz.
Prawda/Fałsz
W podstawie graniastosłupa prostego jest trapez prostokątny. Największy kąt dwuścienny tego
graniastosupa ma miare rowna 150?
Więc największy kąt= 135, więc fałsz.
| 18√3 | ||
h= | = 9√3 | |
| 2 |
| 2 | |
h− szukana odległość | |
| 3 |
| 2 | |
*9√3=6√3 | |
| 3 |
| 72 | 36 | ||
= | |||
| 100 | x |
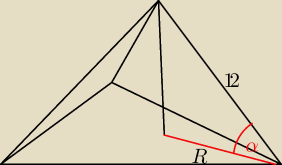 3. Promień okręgu opisanego na podstawie ostrosłupa prawidłowego trójkątnego jest równy 6√3,
a dlugosc krawędzi bocznej 12. Zatem krawędź boczna tego ostrosłupa jest nachylona do
płaszczyzny podstawy pod kątem?
Promień okręgu opisanego to odległość od spodka wysokości do wierzchołka.
R=6√3
3. Promień okręgu opisanego na podstawie ostrosłupa prawidłowego trójkątnego jest równy 6√3,
a dlugosc krawędzi bocznej 12. Zatem krawędź boczna tego ostrosłupa jest nachylona do
płaszczyzny podstawy pod kątem?
Promień okręgu opisanego to odległość od spodka wysokości do wierzchołka.
R=6√3
| 6√3 | √3 | |||
cosα= | = | ⇒ α=30 | ||
| 12 | 2 |
| 12 | 6 | 6√3 | ||||
tgα=U{H}{2√3 = | = | = | = 2√3 | |||
| 2√3 | √3 | 3 |
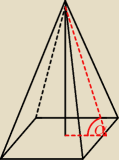 5. W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 6√2 a wysokość 3√6.
Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem?
5. W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 6√2 a wysokość 3√6.
Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem?
| 3√6 | √6 | 2√3 | ||||
tgα= | = | = | = √3 ⇒ α=60 | |||
| 3√2 | √2 | 2 |
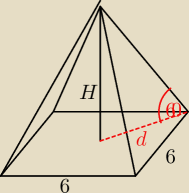 6. W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 6, a krawędź boczna jest
nachylona do płaszczyzny podstawy pod kątem 60. Zatem wysokość tego ostrosłupa ma długośc
równą?
d=3√2
tg60=√3
6. W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 6, a krawędź boczna jest
nachylona do płaszczyzny podstawy pod kątem 60. Zatem wysokość tego ostrosłupa ma długośc
równą?
d=3√2
tg60=√3
| H | ||
√3= | ||
| 3√2 |
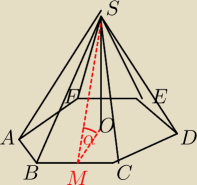 7. Prawda/Fałsz
Na rysunku przedstawiony jest ostrosłup prawidłowy sześciokątny. Jeżeli BC=10 i SO=5√3 to
ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt 45?
MO=5√3
7. Prawda/Fałsz
Na rysunku przedstawiony jest ostrosłup prawidłowy sześciokątny. Jeżeli BC=10 i SO=5√3 to
ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt 45?
MO=5√3
| 5√3 | ||
tgα= | ⇒ α=45 Prawda | |
| 5√3 |
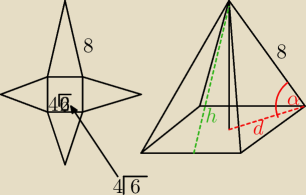 8. Na rysunku przedstawiona jest siatka ostrosłupa prawidłowego czworokątnego. oblicz:
a) miarę kąta zawartego między krawędzią boczną ostrosłupa, a przekątną podstawy
b) długość wysokości ostrosłupa
c) pole powierzchni bocznej ostrosłupa
a) rozumiem, że ten kąt, to ten sam kąt co kąt nachylenia krawędzi bocznej do płaszczyzny
podstawy?
jesli tak, to
8. Na rysunku przedstawiona jest siatka ostrosłupa prawidłowego czworokątnego. oblicz:
a) miarę kąta zawartego między krawędzią boczną ostrosłupa, a przekątną podstawy
b) długość wysokości ostrosłupa
c) pole powierzchni bocznej ostrosłupa
a) rozumiem, że ten kąt, to ten sam kąt co kąt nachylenia krawędzi bocznej do płaszczyzny
podstawy?
jesli tak, to
| 1 | 1 | |||
d= | *4√12 = | *8√3 = 4√3 | ||
| 2 | 2 |
| 4√3 | √3 | |||
cosα= | = | → α = 30 | ||
| 8 | 2 |
| √3 | ||
b) tg30= | ||
| 3 |
| √3 | H | ||
= | |||
| 3 | 4√3 |
| 4√6*2√10 | ||
Pb=4* | = 16√60=32√15 | |
| 2 |
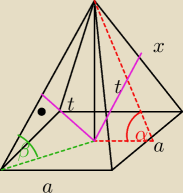 9. W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy
9. W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy
| √6 | ||
pod kątem α takim, że tgα= | . | |
| 3 |
| √6 | ||
tgα= | ||
| 3 |
| √6 | H | ||
= | |||
| 3 | 6√2 |
| 4√3 | √3 | |||
b) tgβ= | = | ⇒ β=30 | ||
| 12 | 3 |
| t | ||
sinβ= | ||
| 12 |
| t | ||
sin30= | ||
| 12 |
| 1 | t | ||
= | |||
| 2 | 12 |
 między innymi na to ostatnie
podpunkt c), reszty jestem w 90% pewien, mimo wszystko z góry dziękuję
między innymi na to ostatnie
podpunkt c), reszty jestem w 90% pewien, mimo wszystko z góry dziękuję 
 Jeżeli czujesz się mimo to urażony− to dziękuję Ci i a7 za sprawdzenie tych dwóch zadan.
Jeżeli czujesz się mimo to urażony− to dziękuję Ci i a7 za sprawdzenie tych dwóch zadan.
 nie
mniej dziękuję
nie
mniej dziękuję 

 więc nawet jak ich nie dostanę na sprawdzianie, to
warto mimo to do matury wiedzieć, czy nie popełniłem tu błędu
więc nawet jak ich nie dostanę na sprawdzianie, to
warto mimo to do matury wiedzieć, czy nie popełniłem tu błędu 


