geometria MalWas: W kwadrat o boku długości 1 wpisano trójkąt, w którym jeden z kątów ma miarę α. Sprawdź czy nierówność P≤sinα, gdzie P oznacza pole trójkąta, jest prawdziwa.

a7:

	1
P=		sinα*ab≤sinα
	2

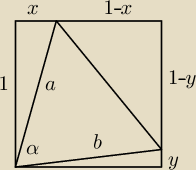
ab≤2 a=√1+x² b=√1+y² √1+x²*√1+y²≤2 (1+x²)(1+y²)≤4 x²+y²+x²*y²≤3 x∊(0,1) i y ∊(0,1) czyli x²<1 i y²<1 to x²y²<1 czyli cała nierówność jest spełniona c.n.u

a7: poprawka x∊(0,1> y∊(0,1> czyli x²*y²≤1 (nierówność nadal jest spełniona przy poprawionych warunkach dla x i y)

MalWas: Dziękuję