Badanie ilości rozwiązań
Patryk: Cześć,
Mam pytanie do poniższego zadania:
Zbadaj liczbę rozwiązac w zależności od wartości "a".
√2|x| −x2 = a
2|x|−x2 = a2 (+ zrobiłem założenia)
Naszkicowałem wykres i dla "a" wyszło mi, że 0 rozwiązań jest dla a ∊(−∞;0)⋁(1;+∞).
Ale ja mam określić rozwiązania dla "a2" więc (−∞;0)⋁(1;+∞) trzeba by podnieść do kwadratu i
według mnie wyszedł by przedział (1;+∞), bo dla <0;1> są inne ilości rozwiązań( 2, 3 i 4
rozwiązania), ale w odpowiedziach mam podane, że 0 rozwiązań jest dla a∊∊(−∞;0)⋁(1;+∞). Moje
pytanie dlaczego tak skoro taki przedział wychodzi mi dla "a" a ja uwzględniam a2
29 lut 15:43
ite: Jakie zrobiłeś założenia?
29 lut 16:03
ite: W zadaniu jest polecenie rozwiąż graficznie?
29 lut 16:05
Patryk: Założenia:
Df = <−2;2> i a ≥0.
Metoda rozwiązania dowolna
29 lut 16:10
Mila:
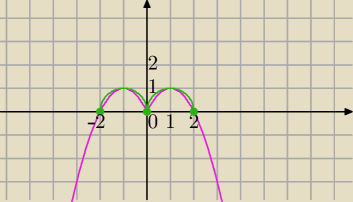
1) a≥0 bo f(x)≥0 dla a<0 brak rozwiązań
tylko dla a≥0 równanie: f(x)=a może mieć rozwiązanie.
2 ) f(x)=
√−x2+2|x|
D:
−x
2+2|x|≥0⇔
−|x|
2+2|x|≥0
|x|*(−|x|+2)≥0⇔
−|x|+2≥0
|x|−2≤0
|x|≤2
x∊<−2,2>
a)
równanie: g(x)=−x
2+2|x|=a
2
−|x|
2+2|x|=a
2 i a≥0 i x∊<−2,2>
a
2>1 i a≥0⇔|a|>1⇔a>1 brak rozwiązań
lub
a
2=1 i a≥0⇔a=1 dwa rozw.
lub
a
2∊(0,1) i a≥0⇔dla a∊(0,1) są 4 rozwiązania
lub
a
2=0⇔dla a=0 są 3 rozwiązania
29 lut 16:11
Patryk: Czyli dobrze myślałem, będzie a>1, bo przecież założenie jest a>1, dzięki

29 lut 16:18
 1) a≥0 bo f(x)≥0 dla a<0 brak rozwiązań
tylko dla a≥0 równanie: f(x)=a może mieć rozwiązanie.
2 ) f(x)=√−x2+2|x|
D:
−x2+2|x|≥0⇔
−|x|2+2|x|≥0
|x|*(−|x|+2)≥0⇔
−|x|+2≥0
|x|−2≤0
|x|≤2
x∊<−2,2>
a)
równanie: g(x)=−x2+2|x|=a2
−|x|2+2|x|=a2 i a≥0 i x∊<−2,2>
a2>1 i a≥0⇔|a|>1⇔a>1 brak rozwiązań
lub
a2=1 i a≥0⇔a=1 dwa rozw.
lub
a2∊(0,1) i a≥0⇔dla a∊(0,1) są 4 rozwiązania
lub
a2=0⇔dla a=0 są 3 rozwiązania
1) a≥0 bo f(x)≥0 dla a<0 brak rozwiązań
tylko dla a≥0 równanie: f(x)=a może mieć rozwiązanie.
2 ) f(x)=√−x2+2|x|
D:
−x2+2|x|≥0⇔
−|x|2+2|x|≥0
|x|*(−|x|+2)≥0⇔
−|x|+2≥0
|x|−2≤0
|x|≤2
x∊<−2,2>
a)
równanie: g(x)=−x2+2|x|=a2
−|x|2+2|x|=a2 i a≥0 i x∊<−2,2>
a2>1 i a≥0⇔|a|>1⇔a>1 brak rozwiązań
lub
a2=1 i a≥0⇔a=1 dwa rozw.
lub
a2∊(0,1) i a≥0⇔dla a∊(0,1) są 4 rozwiązania
lub
a2=0⇔dla a=0 są 3 rozwiązania
