 Zadanie, prośba o potwierdzenie wyniku, sposobu.
https://imgur.com/a/yLHAyY0 zadanie 689
Pk=4πr2
Ps=πa2
3*4πr2=4*πa2
12πr2=4πa2
3r2=a2
a=r√3
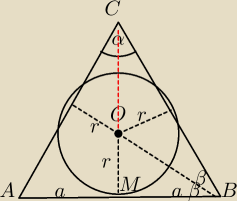
Środek okręgu wpisanego to punkt przecięcia dwusiecznych.
w ΔMBO
Zadanie, prośba o potwierdzenie wyniku, sposobu.
https://imgur.com/a/yLHAyY0 zadanie 689
Pk=4πr2
Ps=πa2
3*4πr2=4*πa2
12πr2=4πa2
3r2=a2
a=r√3
Środek okręgu wpisanego to punkt przecięcia dwusiecznych.
w ΔMBO
| r | r | √3 | ||||
tgβ= | = | = | ||||
| a | r√3 | 3 |
| α | ||
2β+ | +90=180 | |
| 2 |
| α | ||
150+ | =180 | |
| 2 |
| α | |
=30, więc α = 60 | |
| 2 |
| 1 | ||
PΔ= | *l*l*sin90 | |
| 2 |
| 1 | ||
27= | l2 | |
| 2 |
| 1 | ||
V= | *π*(3√32*3√3= 27√3π | |
| 3 |
| 4πr2 | 4 | r2 | 1 | ||||
= | ⇔ | = | |||||
| πR2 | 3 | R2 | 3 |
| r | 1 | ||
=tgβ= | |||
| R | √3 |
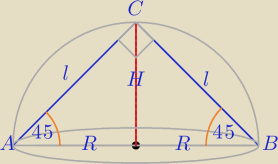 Z2) też krócej można
Z2) też krócej można
| 1 | ||
1) PΔABC= | *l2 (Połowa kwadratu o boku l) | |
| 2 |
| 1 | |
*l2=27 ⇔l2=54⇔l=3√6 | |
| 2 |
| 1 | ||
V= | *π*(3√3)2*3√3 | |
| 3 |
