trygonometria salamandra: Rozwiąż nierówność −2sin3x≥1 w przedziale <0;2π>

	1
sin3x≤
	2

	−π
3x=		+2kπ
	6

	−π		2
x=		+		kπ
	18		3

lub

	π
3x=π−(−		)+2kπ
	6

	7
3x=		π+2kπ
	6

	7		2
x=		π+		kπ
	18		3

no i pytanie czy mogę polegać na takiej mojej "metodzie"

	−π
Wiem, że od		to 0 na pewno będzie funkcja rosła, a raczej aż do następnego miejsca
	18

	−1
zerowego równania sin3x=		, więc nie rozpatruję tego miejsca zerowego, tylko biorę
	2

następne,

	7
czyli		π. Od tego miejsca, do następnego miejsca zerowego sin3x=−1/2, na pewno wartości
	18

będą mniejsze od −1/2.

	−π		2		11		7
Biorę k=1, czyli x=		+		π=		π, więc pierwszy przedział <		π;
	18		3		18		18

	11
		π>
	18

	7		2
Później ta sama zabawa, czyli k=1, ale dla drugiego rozwiązania, czyli		π+		π =
	18		3

	19
		π
	18

	23
k=2 dla pierwszego: x=		π
	18

	19		23
drugi przedział: <		π;		π>
	18		18

	31
k=2 dla drugiego: x=		π
	18

	35
k=3 dla peirwszego x=		π
	18

	31		35
trzeci przedział: <		π;		π>
	18		18

	11		19		23		31
Suma przedziałów: x∊<U{7}{18π;		π> U <		π;		π> U <		π;
	18		18		18		18

	35
		π>
	18

wredulus_pospolitus: gdzie zniknął minus z pierwotnej postaci nierówności

salamandra:

	−1
Oczywiście		, uciekł mi pisząc tu
	2

wredulus_pospolitus:

salamandra: Rozwiązanie mam ok, pytałem tylko o sposób, jakbym nie chciał robić rysunku, bo dla 3x to już znacznie się zwęża. Nauczyciel kiedyś pokazywał mi sposób, żeby narysować pomocniczy wykres

	−1
sinx, obliczyć miejsca zerowe (w tym przypadku sinx=		) a później po prostu odpowiednio
	2

podzielić/pomnożyć, w tym wypadku podzielić, ale nie pamiętam czy tak dokładnie to było.

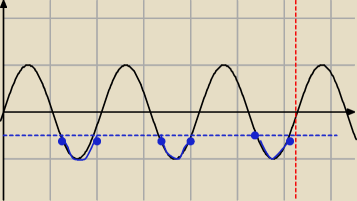
wredulus_pospolitus: to Ci przypomnę 1) rysujesz y = sinx 2) obszar okresu podstawowego ( czyli <0;2π>) dzielisz na '3' równe części 3) w każdej tych części masz 'zmieścić wykres sinx' jak widzisz na wykresie powyżej −−− dokładnie trzy okresy będą w przedziale <0;2π>

wredulus_pospolitus: metoda dobra ... ale brakuje mi podstawowej rzeczy

	7		11
3x ∊ <		π + 2kπ ;		π + 2kπ> <−−− czyli to na podstawie czego wypisujesz później
	6		6

przedziały De facto nigdzie nie pokazałeś jak rozwiązałeś tą NIERÓWNOŚĆ ... wypisałeś tylko punkty dla których zachodzi równość i później (magicznie) pojawiają się przedziały

salamandra: Dzięki

salamandra: No tak jak mówiłem, wiem, że od zera do pierwszego "punktu" funkcja będzie miała wartości

	7
powyżej −1/2, dopiero od		π spadnie poniżej 1/2 i będzie miała wartości ≤ −1/2 aż do
	18

drugiego "punktu" i pozniej analogicznie

wredulus_pospolitus: A tak zmieniając temat ... jak tam tamta praca domowa? Oddane bez problemów?

wredulus_pospolitus: salamandra ... to że 'wiesz' to jedno ... ale to trzeba napisać (i nie SŁOWNIE, tylko podać po prostu przedział)

salamandra: Sprawdzona, sprawdzona ale bez Was bym nie dał rady