| (m+1)x−2 | ||
Wyznacz wszystkie wartości parametru m dla których funkcja wymierna F(x)= | ||
| x−m |
| m2+m−2 | ||
Wiem ze trzeba przeksztalcic do kanonicznej : F(x) = m+1+ | ||
| x−m |

 Więc mianownik będzie przez pewien (długi czas) mniejszy od zera a później większy od zera
Więc mianownik będzie przez pewien (długi czas) mniejszy od zera a później większy od zera 
 I to bez względu na to jaki 'm' by się nie podstawiło.
I to bez względu na to jaki 'm' by się nie podstawiło.
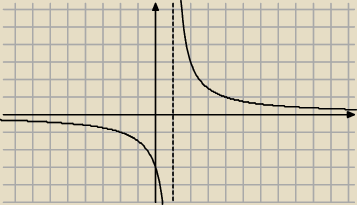 no będzie ... ale to nas nie interesuje ... zauważ, że funkcja homograficzna ma jedną z dwóch
postaci:
a) dla licznika > 0
no będzie ... ale to nas nie interesuje ... zauważ, że funkcja homograficzna ma jedną z dwóch
postaci:
a) dla licznika > 0
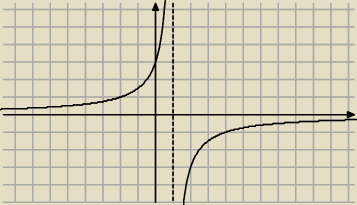 b) dla licznika < 0
b) dla licznika < 0
 ciagle myslalem ze to zalezy rowniez od mianownika a nie tylko licznika
a przeciez licznik w postaci kanonicznej jest staly tj nie ma X
ciagle myslalem ze to zalezy rowniez od mianownika a nie tylko licznika
a przeciez licznik w postaci kanonicznej jest staly tj nie ma X