Ostrosłupy Marcinkiewicz: Przekrój ostrosłupa prawidłowego trójkątnego ABCS płaszczyzną przechodzącą przez wierzchołek S i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa

	4√3
ma długość		. Oblicz objętość tego ostrosłupa.
	3

wredulus_pospolitus:

	4√3		2√3
2a =		−> a =
	3		3

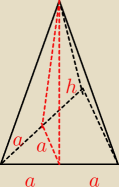
z treści zadania wiemy, że a = h H_ostrosłupa = √h² − (h_podstawy/3)² = Wyznaczasz. Podstawiasz do wzoru na objętość ostrosłupa i gotowe

Marcinkiewicz:

	4√3
jeszcze raz, skąd wiadomo, żę 2a to		?
	3

wredulus_pospolitus: Ach ... krawędź boczna ... sorki −−− no to wyznacz z trójkąta prostokątnego wartość 'a'

	4√3
a2 + a2 = (		)2
	3

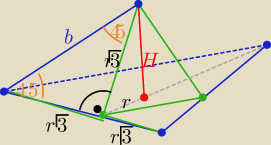
a@b: H²=3r²−r² ⇒ H=r√2

	4√3
b=r√3*√2 =		⇒ r=2√2/3 to r2=8/9 to H=4/3
	3

P_p= 3r²√3 to V= r²√3*H =.....

	32√3
V=
	27

========

Marcinkiewicz: wytłumaczysz a@b jak to się stało?