Ciąg (a_n) określony jest wzorem a_n = n + (n + 1) + (n + 2) + (n + 3) + ... + 2 orion: Ciąg (a_n) określony jest wzorem a_n = n + (n + 1) + (n + 2) + (n + 3) + ... + 2n. Oblicz najmniejszy wyraz ciągu (a_n) większy od 1890.

ite:

	n * (1 + n)
an = n + (n + 1) + (n + 2) + (n + 3) + ... + (n + n) = n * (n + 1) +		=
	2

= 1,5*(n * (n + 1)) 1,5*[n * (n + 1)]>1890

orion:

	3n2 + 3n
1,5*(n2+n) =
	2

3n2 + 3n		2
	> 1890 / *
2		3

n² + n − 1260 > 0 zał. n ∊ ℕ⁺ Δ = 1 + 5040 = 5041 √5041 = 71

	−1 − 71
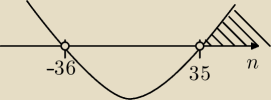
n1 =		= −36 < 0 ∉ ℕ+
	2

	−1 + 71
n2 =		= 35 ∊ ℕ+ ⇒ n > 35
	2

	3 * 362 + 3 * 36
n36 =		= 1998
	2

Bardzo dziękuję