stereometria
salamandra: Trójkąt równoramienny o obwodzie p, którego kąt przy wierzchołku ma miarę 2α obraca się dookoła
podstawy. Oblicz objętość powstałej bryły jeśli α=60 i p=12
https://imgur.com/a/mCt1eId
Potwierdziłby mi ktoś? (w linku są dwa zdjęcia)
26 lut 15:50
wredulus_pospolitus:
czemu połowa obwodu trójkąta = bok + połowa podstawy + wysokość trójkąta

26 lut 16:38
salamandra: dobre pytanie, nie wiem co miałem na myśli robiąc to

26 lut 16:41
Mila:
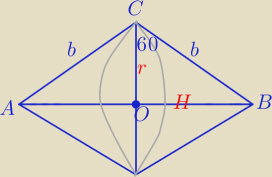
|AB|=a,
1) 2b+a=12
2b+b
√3=12
b*(2+
√3)=12 /*(2−
√3)
b=12*(2−
√3),
a=12
√3*(2−
√3)
2)
|OC|=6(2−√3)=r
H=6√3*(2−√3)
| | 1 | | 1 | |
Vs= |
| *πr2*h= |
| *π*(6(2−√3))2*6√3*(2−√3) |
| | 3 | | 3 | |
V
s=72π*(26
√3−45)
V
b=144π*(26
√3−45)
===============
26 lut 16:41
salamandra: no to mam źle po korekcie:
| | | | 6−4√3 | |
r= |
| = |
| = (6−4√3)*(−3)=−18+12√3 = |
| | | | | |
6(2
√3−3)
6
√3(2
√3−3)=3h / :3
2
√3(2
√3−3)=h
12−6
√3=h
Pp=π*(6(2
√3−3))
2
Pp=π*(12
√3−18)
2
Pp=π*(432−432
√3+324)
Pp=756π−432
√3π = 108π(7−4
√3)
| | 1 | |
V= |
| *108π(7−4√3)*(12−6√3) = 36π(7−4√3)(12−6√3)= |
| | 3 | |
= 36π(156−90
√3)
26 lut 17:31
salamandra:
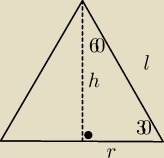
Nie wiem czemu nie dodał się rysunek
26 lut 17:33
salamandra: Czy ja aby źle go obróciłem, jak typowego stożka (wokół osi symetrii)? Dopiero teraz
zrozumiałem Twój rysunek Milu, dziwiłem się czemu takie coś narysowałas.
26 lut 18:16
salamandra: Już wyszło jak należy

26 lut 18:45
Mila:

To dobrze.
26 lut 21:53
salamandra: Pytanie jedynie mam, jak mam 1872√3π−3240π=72π(26√3−45) to jak znaleźć tę największą liczbę
którą wynosimy przed pierwiastek? Również zawsze ubolewam jak mam jakiś duży pierwiastek i jak
szukam co mogę wynieść, to sprawdzam po kolei, czy dzieli się przez 4,9,16,25 itp, jest na to
jakiś algorytm?
26 lut 21:57
Mila:
Różnie można :
1) Na piechotę: dzielę kolejno przez wspólny dzielnik, taki jaki "widzę":
1872:4=468
3240:4=810
468:9=52
810:9=90
1872√3π−3240π=(4*9)π*(52√3−90)=36*2*(26√3−45)
2) rozkład liczb na czynniki pierwsze i wyznaczenie NWD
3) Algorytm Euklidesa
NWD(1872,3240)=NWD(3240−1872, 1872)=
=NWD(1368, 1872)=NWD(504, 1368)=
=NWD(864,504)=NWD(360,504) =NWD(144,360)=...itd ....=72
26 lut 22:36
salamandra: dziękuję
26 lut 22:41


 |AB|=a,
|AB|=a,
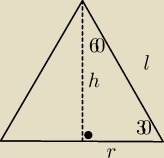 Nie wiem czemu nie dodał się rysunek
Nie wiem czemu nie dodał się rysunek

 To dobrze.
To dobrze.