planimetria salamandra: Udowodnij, że: a) przekątne rombu są jednocześnie dwusiecznymi b) przekątne równoległoboku przecinają się w połowie z tym b) to dla mnie to logiczne, tylko nie wiem jak to ubrać w słowa lub zrobić to algebraicznie, a z a) nie wiem

ite : a/ dobry rysunek (= ratunek w każdej sytuacji) narysuj jedną przekątną rombu na początek, jak zobaczysz trójkąty równoramienne, to sukces będzie blisko

Jerzy: a) wskazowka: w każdym rombie przekątne są prostopadłe i się połowią.

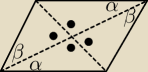
salamandra: Nie wiem co dalej

ite : salamandra dobry rysunek − to taki, który przedstawia analizowaną figurę a nie jakąś inną. Masz udowodnić własność rombu, a rysujesz równoległobok! Nie każdy równoległobok jest rombem!

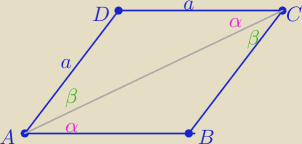
a@b: ΔACD równoramienny to β=α zatem AC −− jest dwusieczną Analogicznie dla kąta ABC

Jerzy: To nie jest romb.

salamandra: w równoległoboku nie przecinają się pod kątem prostym, więc to jest romb nie wiem jak mam tu odmierzyć te odcinki, nigdy mi nie wyjdzie równo.

salamandra: dzięki a@b, nie wiedziałem, że to takie banalne...

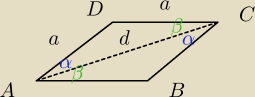
ite : Na właściwym rysunku widać, że obu boki trójkątów są odpowiednio równe oraz że oba są równoramienne.

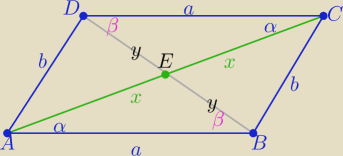
a@b: Oznaczenia jak na rys dopisz komentarz ......... to ΔABE i CDE są przystające z cechy (kbk) zatem |DE|= |BE| i |AE|=|CE| co kończy dowód

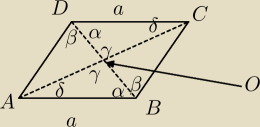
salamandra: ABO i DCO przystające, więc AO=CO, wystarczy? (do b)

salamandra: Potwierdźcie mi jeszcze, bo chce raz na zawsze zapamiętać− środek okręgu opisanego na wielokącie wyznaczają symetralne boków (punkt ich przecięcia), środek okręgu wpisanego w wielokąt− punkt przecięcia dwusiecznych. Oraz skąd wynika, że w trójkącie (tylko równobocznym?) środek okręgu opisanego i wpisanego jest w tym samym miejscu?

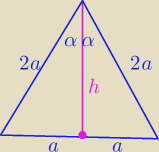
a@b: h −− jest i symetralną i dwusieczną i wysokością tylko w Δ równobocznym Jestem w ,że zadajesz takie pytanie ( na poziomie 5kl. SP

salamandra: miałem dylemat jak to będzie w równoramiennym