Oblicz sumę wszystkich miejsc zerowych funkcji Michał: Oblicz sumę wszystkich miejsc zerowych funkcji f(x)=sin2x należących do przedziału <0;20π> Proszę o pomoc

Leszek: sin(2x) = 0 ⇒ 2x = kπ ⇒ x= kπ/2 Dokoncz !

Pat: sin2x=0 w <0,20π> 2x=0+^kπ₂ gdzie k∊C x=0+^kπ₄ x₁=0 x₂=^π₄ x₃=^π₂ x₄=^3π₄ Zauważamy, że to ciąg arytmetyczny a_n=a₁+(n−1)r r=^π₄ a₁=^π₄ a_n=20π − bo to ostatni wyraz 20π=^π₄+(n−1)^π₄ → n=80 Suma wyrazów ciągu arytmetycznego: S_n=(^π₄+20π)*¹₂*80 S_n=810π Proszę o sprawdzenie.

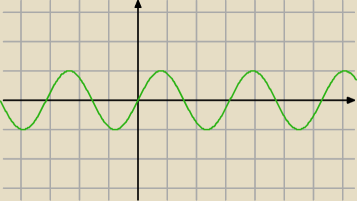
a7: y=sin2x x₁=π/2 r=π/2

Pat: Faktycznie, przepraszam sinx=0 dla x=π więc x₁=^π₂ jak a7

Jerzy: A dlaczego x₁ = π/2 ?

Jerzy: Pat,nie bredź.sin2x = 0 ⇔ x = kπ/2

a7:

	π		π		π
x1=π/2 r=π/2 xn=20π =π/2+(n−1)*(π/2) czyli n=40 (obliczamy 20π=		+n		−
	2		2		2

stąd n=40)

Jerzy: x₁ = 0 , a nie π/2

a7: no tak czyli n=41

a7: x₁=0 r=π/2 x_n=20π x_n=x₁+(n−1)r

	π		π
20π=n*		−
	2		2

41		π
	π=n*
2		2

n=41

Pat: Jerzy, przecież napisałem i się poprawiłem. n=40 jak nie liczymy zera, wtedy wzór na sumę ciągu S₄₁=(0+20π)*¹₂*41 n=41 jak liczymy zero, wtedy wzór na sumę ciągu S₄₀=(^π₂+20π)*¹₂*40 S₄₀=S₄₁

Jerzy: Pat, 13:58 sinx = 0 ⇔ x = π , jest neprawdą bez dodatkowych założeń.