okrąg salamandra: Wyznacz równanie okręgu przechodzącego przez punkty A(−5,3) i B(0,6) którego środek lezy na prostej o równaniu x−3y+1=0

	17√10
Chciałem policzyć promień na odległość punktu od prostej i wychodzi mi r=		czyli
	10

	289
r2=		,a
	10

	289
w odpowiedzi jest r2=		, więc już na tym etapie coś zepsułem.
	9

	1		1
Mając promień, wyznaczyłem S(x,		x+		) i liczyłem odległość (równą promieniowi) S od
	3		3

któregoś z punktów i również źle wyszło.

bezendu: Jeśli środek lezy na tej prostej to S(3y−1,y) (3y+4)²+(y−3)²=(3y−1)²+(y−6)²

salamandra: No to w zasadzie to samo, tylko ja „x” liczyłem czyli muszę przyrównać dwie odległości? Nie moge skorzystać ze wzoru na odległość prostej od punktu?

bezendu: Skoro punkt lezy na środku okręgu i pubkty należą do tego okręgu, to odległość między AS i BS jest taka sama

salamandra: No tak, rozumiem, a mógłbyś jeszcze wyjaśnić dlaczego nie oblicze poprawnie promienia korzystając ze wzoru na odległość prostej na której leży środek od punktu A lub B?

Patryk: Salamandra, tak z ciekawości zapytam, których działów masz jeszcze nie opanowanych do maturki? Ja teraz jestem przy stereometrii, a później pochodne, optymalizacja i prawdopodobieństwo.

salamandra: Nieopanowanych, że jeszcze ich na lekcji nie przerabiałem, czy z czego czuję, że kuleję?

Patryk: Powiedzmy najpierw, których nie miałeś na lekcji.

salamandra: od jutra zaczynamy najprawdopodobniej bryły obrotowe (walec, stozek, kula), a później prawdopodobieństwo i kombinatoryka

Patryk: A pochodne i optymalizacje macie za sobą już?

salamandra: Pochodną w 3 klasie miałem, teraz mam optymalizację stricte do stereometrii, wcześniej miałem optymalizacje podczas planimetrii

Patryk: Hmm... to masz lepszą sytuacje ode mnie. U mnie jest więcej nieruszonych tematów

salamandra: No, a czasu jest naprawdę bardzo mało.... mam ten zbiór kiełbasy, ale powiem Ci szczerze, że jest tyle do nauki na bieżąco z tej stereometrii, szczególnie ze na początku nic nie ogarniałem, że nie miałem czasu przez prawie cały luty solidnie robić tej książki, zwykle x godzin spędzam po szkole na robieniu zadań ze stereometrii, wiec nie wiem jak to będzie. Całej na pewno już nie zdążę przerobić.

Patryk: Ja też przypuszczam, że się nie wyrobię z Kiełbasą, działy robię po kolei, jestem przy stereometrii a muszę jakieś 3 tyg zostawić na ogarnianie arkuszy maturalnych z poprzednich lat więc po prostu ile zdążę zrobić to zdążę. Najwyżej jak nie wyrobię się z prawdopodobieństwem to na jakieś korki pójdę i tyle

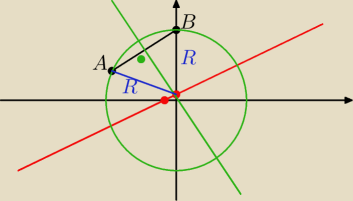
an: Moim zdaniem Matematykę, fizykę trzeba zrozumieć to wszystko się zazębia nie znasz podstaw, może coś nauczysz się na pamięć, ale "jakieś drobne inaczej" i jest problem Przykładowo to zadanie w skrócie. Punkty AB leżą na okręgu PODSTAWA odcinek AB jest cięciwą tego okręgu PODSTAWA na siecznej cięciwy leży środek okręgu WNIOSEK mamy prostą przechodzącą przez środek okręgu jeżeli wyznaczymy sieczną danej cięciwy AB to punkt ich przecięcia jest szukanym środkiem okręgu a jego odległość od punktów A lub B promieniem okręgu robimy szkicowy rysunek (pomocna GOGEBRA) i obliczenia i tak "mniej więcej" rozwiązywanie powinna wyglądać. Ogarnięcie podstaw zajmie ci kilka dni, ale zaoszczędzisz potem dużo czasu i jeżeli pójdziesz na kierunek w jakikolwiek sposób związany z matematyką nie będziesz musiał się tego uczyć

salamandra: Boje się zadawać pytania, żebyś znowu mi nie powiedział, że nie znam podstaw, ale niech stracę Rozumiem to co zrobiles, jednak 1. czemu ta sieczna jest prostopadła do cięciwy, 2. Skąd wiesz w którym miejscu na cieciwie AB będzie punkt przecięcia cięciwy z sieczna? Czy to wynika z tego, ze powstaje niejako trojkat równoramienny wiec wysokość podzieli AB na polowe?

an: Ta "sieczna" poprawnie powinno być to symetralna cięciwy

salamandra: Reszta tak jak powiedziałem?

salamandra: Reszta tak jak powiedziałem?

an: Tak, symetralna jest prostopadła do odcinka (w tym wypadku cięciwy) i dzieli go na dwie równe części i przechodzi przez środek okręgu, przy okazji przyszłościowo dzieli ten łuk okręgu oparty na tej cięciwie na dwie równe części, jest prostopadła do stycznej do łuku w tym punkcie.