matematykaszkolna.pl
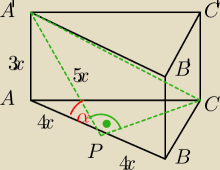
Punkt P jest środkiem krawędzi AB graniastosłupa prawidłowego trójkątnego. Ewcia34: Punkt P jest środkiem krawędzi AB graniastosłupa prawidłowego trójkątnego. Graniastosłup ten przecięto płaszczyzną CPA' , która jest nachylona do płaszczyzny podstawy graniastosłupa (ABC) pod kątem α . W przekroju otrzymano trójkąt o polu powierzchni 640√3. sinα = 3/5 Oblicz |PC| i objętość tego graniastosłupa.
23 lut 19:26
salamandra: Podasz odpowiedź? Bo nie chcę bezsensownie błędnych obliczeń wysyłać w razie co
23 lut 19:43
Ewcia34: nie mam odpowiedziemotka
23 lut 21:08
salamandra: rysunekTo najwyżej ktoś potwierdzi:
 3 
sinα=
 5 
PC=4√3x PA'PC=640√3
 1 
640√3=
*3x*4√3x
 2 
640√3=6√3x2 640=6x2
 8√15 
x=
 3 
|PC|=32√5
 5120√3 
Pp=
 3 
V=40960{5}
23 lut 21:49
salamandra: V=40960√5
23 lut 21:54
an: Ma być policzone pole ΔA`BC, a jest
23 lut 22:55
salamandra: Gdzie tak jest powiedziane?
23 lut 22:57
an: Chodzi mi o ΔA`PC nie ΔA`BC
23 lut 23:02
salamandra: "W przekroju otrzymano trójkąt o polu powierzchni 640√3." To nie jest to? emotka?
23 lut 23:02
an: Tak , a co tam wyliczyłeś
23 lut 23:06
salamandra: Pp=PABC
23 lut 23:09
salamandra: Ok, już widzę błąd chyba.
23 lut 23:10
salamandra:
 1 
640√3=
*5x*4√3x
 2 
a ja napisałem 3x
23 lut 23:11
an: 640√3=1/2*3x*4√3x2 co tu jest policzone
23 lut 23:12
an: tak
23 lut 23:12
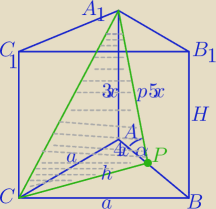
Mila: rysunek a=8x
 3 
sinα=
 5 
 8x√3 
1) |PC|=
=4x√3
 2 
 1 1 
2) PΔCPA1=
*h*p=
*4x√3*5x=10x2√3
 2 2 
10x2√3=640√3 x2=64 x=8 a=64 H=24 2) |PC|=32√3
 642√3 
V=
*24
 4 
V=24576√3 ==========
23 lut 23:12
salamandra: 640√3=10√3x2 640=10x2 64=x2 x=8
 64√3 
Pp=
= 16√3
 4 
H=3x= 18 V=16√3*18 = 288√3
23 lut 23:12
salamandra: Tfu.... a=8x a=64
 642√3 4096√3 
więc Pp=
=
= 1024√3
 4 4 
H=3x= 24, a nie 18 więc V=1024√3*24= 24576√3
23 lut 23:15