Stereometria
Patryk: Witam,
Czy mógłby mi ktoś wskazać gdzie znajduje się kąt pomiędzy przekątną ściany bocznej a sąsiednią
ścianą boczną w graniastosłupie prawidłowym trójkątnym? I czy zna ktoś sposób jak sobie takie
kąty wyobrażać? Jakiś sposób, który pomógł by wyobrazić tego typu kąty.
23 lut 17:45
23 lut 17:59
Mila:
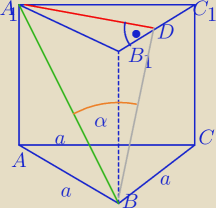
α− kąt między przekątną BA
1 a ścianą boczną BCC
1B
1
( kąt między BA
1 i jej rzutem prostokątnym na ścianę BCC
1B
1)
23 lut 18:01
piotrek: kąt BDA1 = π/2
23 lut 18:04
Patryk: Dzięki wielkie! Mila, masz jakieś sposoby na zauważanie takich kątów czy po prostu trzeba się
poszczególnych sytuacji uczyć na pamięć?
23 lut 18:47
a@b:
23 lut 19:04
a@b:
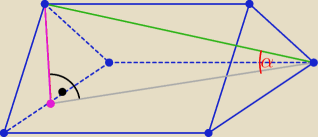
Postaw ten graniastosłup na ścianie
Czy tak ładniej widać ten kąt?
23 lut 19:05
salamandra:
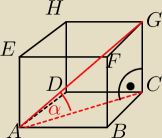
Patryk, mi dużo pomogło jak nauczyciel mi tłumaczył to na takiej zasadzie, weźmy pod lupę− kąt
między przekątną sześcianu, a płaszczyzną podstawy.
Punkt A już leży na podstawie, więc jest odbiciem samego siebie, punkt G nie leży na podstawie,
więc go rzutujemy− jego odbiciem będzie punkt C, i tam będzie kąt prosty.
W Twoim przykładzie− punkt B już jest na ścianie bocznej, więc jest odbiciem samego siebie, a
punkt A (wierzchołek trójkąta) rzutujemy na tę ścianę pod kątem prostym, a z wierzchołka pod
kątem prostym wychodzi wysokość! stąd A
1D to wysokość podstawy!
23 lut 19:30
Patryk: Dobra, ogarnę jakoś, dzięki za pomoc

23 lut 21:50
23 lut 23:23
grafik:
A Mila wciąż krawędzie niewidoczne rysuje linią ciągła, a widoczne przerywaną

23 lut 23:31
Mila:
To popraw grafiku.
23 lut 23:55
 α− kąt między przekątną BA1 a ścianą boczną BCC1B1
( kąt między BA1 i jej rzutem prostokątnym na ścianę BCC1B1)
α− kąt między przekątną BA1 a ścianą boczną BCC1B1
( kąt między BA1 i jej rzutem prostokątnym na ścianę BCC1B1)

 Patryk, mi dużo pomogło jak nauczyciel mi tłumaczył to na takiej zasadzie, weźmy pod lupę− kąt
między przekątną sześcianu, a płaszczyzną podstawy.
Punkt A już leży na podstawie, więc jest odbiciem samego siebie, punkt G nie leży na podstawie,
więc go rzutujemy− jego odbiciem będzie punkt C, i tam będzie kąt prosty.
W Twoim przykładzie− punkt B już jest na ścianie bocznej, więc jest odbiciem samego siebie, a
punkt A (wierzchołek trójkąta) rzutujemy na tę ścianę pod kątem prostym, a z wierzchołka pod
kątem prostym wychodzi wysokość! stąd A1D to wysokość podstawy!
Patryk, mi dużo pomogło jak nauczyciel mi tłumaczył to na takiej zasadzie, weźmy pod lupę− kąt
między przekątną sześcianu, a płaszczyzną podstawy.
Punkt A już leży na podstawie, więc jest odbiciem samego siebie, punkt G nie leży na podstawie,
więc go rzutujemy− jego odbiciem będzie punkt C, i tam będzie kąt prosty.
W Twoim przykładzie− punkt B już jest na ścianie bocznej, więc jest odbiciem samego siebie, a
punkt A (wierzchołek trójkąta) rzutujemy na tę ścianę pod kątem prostym, a z wierzchołka pod
kątem prostym wychodzi wysokość! stąd A1D to wysokość podstawy!

