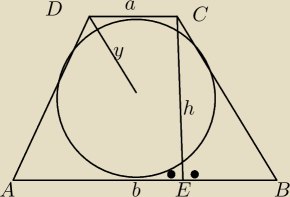
 Na okręgu opisano trapez równoramienny o ramieniu długości 30. Odcinek łączący środek
okręgu z wierzchołkiem przy kącie rozwartym ma długość 18. Oblicz pole tego trapezu.
a+b=c+d −−−> a+b=60
P=1/2(a+b)h=30h
h=2r, y=18
|AD|=|CB|=30
|EB|=b−a/2
r=?
jak tu najkorzystniej wyznaczyć r?
Na okręgu opisano trapez równoramienny o ramieniu długości 30. Odcinek łączący środek
okręgu z wierzchołkiem przy kącie rozwartym ma długość 18. Oblicz pole tego trapezu.
a+b=c+d −−−> a+b=60
P=1/2(a+b)h=30h
h=2r, y=18
|AD|=|CB|=30
|EB|=b−a/2
r=?
jak tu najkorzystniej wyznaczyć r?
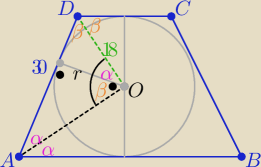 2α+2β=180o ⇒ α+β=90o
AO i DO −−− dwusieczne ( bo okrąg wpisany)
zatem ΔAOD jest prostokątny
z tw. Pitagorasa |AO|= ..... = 24
2α+2β=180o ⇒ α+β=90o
AO i DO −−− dwusieczne ( bo okrąg wpisany)
zatem ΔAOD jest prostokątny
z tw. Pitagorasa |AO|= ..... = 24
| 18*24 | ||
to r= | =... | |
| 30 |