Nierówność, logarytmy
Szkolniak: Rozwiąż graficznie nierówność: log
x(log
yx)>0
Określam dziedzinę:
x>0 ∧ x≠1 ∧ log
yx>0 ∧ y>0 ∧ y≠1
log
yx>0 ⇔ log
yx>log
y1 ⇔ x>1
stąd dziedzina: x>1 ∧ y∊(0;1)∪(1;+
∞)
log
x(log
yx)>0
log
x1−log
x(log
xy)>0
log
x(log
xy)<0 ⇔ log
x(log
xy)<log
x1 ⇔ log
xy<x ⇔ x
x>y
teraz rysujemy wykres funkcji f(x)=x
x i wyciągamy część wspólną z dziedziną oraz z wykresem
funkcji f?
22 lut 23:03
wredulus_pospolitus:
co do dziedziny:
log
yx>0 ⇔ log
yx >log
y1 <−−−− nad interpretacja

a co jeżeli y = 0.5

22 lut 23:08
wredulus_pospolitus:
podobną nadinterpretację robisz później rozwiązując
log
x(log
xy) < log
x1 wcale nie musi być równoznaczne z log
xy < 1 (bo co jeśli x < 1

)
22 lut 23:15
Szkolniak: Wtedy x<1? I w takim razie jakaś wskazówka jak powinno wyglądać określenie dziedziny?
22 lut 23:15
Szkolniak: chodzi o to że jest to związane ze zmianą znaku nierówności i muszę rozpatrzeć dwa przypadki:
dla x∊(0;1) i dla x>1?
22 lut 23:18
wredulus_pospolitus:
Dziedziną ... dwuetapowo
1) dla x > 1 mamy:
logx(logyx) > 0 ⇔ logx(logyx) > logx1 ⇔ logyx > 1 −−−> 1 < y < x (ponieważ dla y<1
mamy logyx < 0 (no bo x>1) ... dla y>x>1 mamy logyx < logyy = 1)
2) dlx x ∊ (0;1) mamy:
logx(logyx) > 0 ⇔ logyx <1 −−−> y>1 (na pewno ... bo wtedy logyx < 0) ale jeszcze może
być 1 > y > x ... bo wtedy logyx < logyy = 1 (bo dla y<1 funkcja logyx jest funkcją
malejącą)
22 lut 23:23
wredulus_pospolitus:
ale Ty to masz wyznaczyć GRAFICZNIE

22 lut 23:24
wredulus_pospolitus:
oczywiście błąd zrobiłem
dla x∊(0;1)
logyx < 1 −−−> y < 1 (bo dla y>1 mamy logyx < 0 <−−− nie spełnia pierwotnego warunku dla
liczby logarytmowanej: logyx > 0)
natomiast jeżeli x < y < 1 to logyx > logyy = 1
więc musi być 0 < y < x < 1
22 lut 23:33
Szkolniak: twój wpis z 23:33
dlaczego dla y>1 mamy logyx<0? próbowałem przeanalizować, ale nie wiem skąd to wnioskujesz
22 lut 23:39
wredulus_pospolitus:
Może chodziło o graficzne zaprezentowanie rozwiązania

Co nie


To by miało wtedy sens.
22 lut 23:39
wredulus_pospolitus:
dla y> funkcja f(x) = log
yx jest funkcją rosnącą tak

Tak (podstawa logarytmu większa o 1 to
funkcja rosnąca)
w takim razie skoro x<1 to:
log
yx < log
y1 = 0
22 lut 23:40
wredulus_pospolitus:
na początku miało być: "dla y>1 ...."
22 lut 23:40
a@b:
log
x(log
yx)>0
D: x>0 i x≠1 i y>0 i y≠0
i log
yx>0 ⇒ 1/ dla y∊(0,1) x<1 2/ dla y>1 x>1
D: x∊(0,1)U(1,
∞) i y∊(0,1)U(1,
∞)
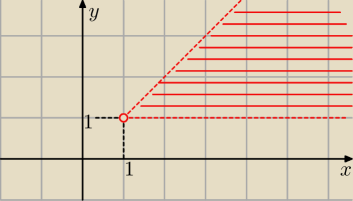
Rozważamy przypadki
1/ x∊(1,
∞) i y∊(1,
∞) to: log
yx>1 ⇒
y<x −−− rys wyżej
2/ x∊(1,
∞) i y∊(0,1) to log
yx<1 ⇒ y>x −− sprzeczność
3/ x∊(0,1) i y∊(1,
∞) ........ sprzeczność
4/ x∊(0,1) i y∊(0,1) ........ sprzeczność
23 lut 02:04
wredulus_pospolitus:
a@b
4) niby czemu sprzeczność

y = 2
−2 ; x = 2
−1
log
x(log
yx) = −log
2(log
22 2) = −log
2(0.5*log
22) = −log
2 2
−1 = 1 > 0
23 lut 02:36
a@b:
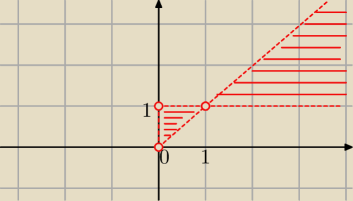
4/ log
yx<1 ⇒ y>x
Teraz pasuje ?

Dobranoc

23 lut 02:47
a@b:
No i masz "muszkę" do smokingu na jutrzejszy dzień

23 lut 02:50
wredulus_pospolitus:
pragnę zauważyć, że y = 2
−2 = 0.25 < 0.5 = 2
−1 = x
więc jak już to 0<y<x

23 lut 02:55
a@b:
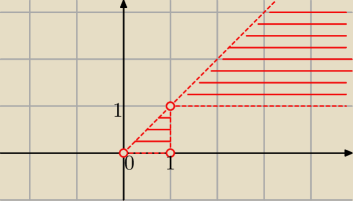
Jasne,że y<x ( to wpływ późnej pory prawie 3:00

23 lut 15:07
Szkolniak: Rozumiem już, dziękuję

25 lut 20:09
 a co jeżeli y = 0.5
a co jeżeli y = 0.5 
 )
)

 Co nie
Co nie 
 To by miało wtedy sens.
To by miało wtedy sens.
 Tak (podstawa logarytmu większa o 1 to
funkcja rosnąca)
w takim razie skoro x<1 to:
logyx < logy1 = 0
Tak (podstawa logarytmu większa o 1 to
funkcja rosnąca)
w takim razie skoro x<1 to:
logyx < logy1 = 0
 logx(logyx)>0
D: x>0 i x≠1 i y>0 i y≠0
i logyx>0 ⇒ 1/ dla y∊(0,1) x<1 2/ dla y>1 x>1
D: x∊(0,1)U(1,∞) i y∊(0,1)U(1,∞)
Rozważamy przypadki
1/ x∊(1,∞) i y∊(1,∞) to: logyx>1 ⇒ y<x −−− rys wyżej
2/ x∊(1,∞) i y∊(0,1) to logyx<1 ⇒ y>x −− sprzeczność
3/ x∊(0,1) i y∊(1,∞) ........ sprzeczność
4/ x∊(0,1) i y∊(0,1) ........ sprzeczność
logx(logyx)>0
D: x>0 i x≠1 i y>0 i y≠0
i logyx>0 ⇒ 1/ dla y∊(0,1) x<1 2/ dla y>1 x>1
D: x∊(0,1)U(1,∞) i y∊(0,1)U(1,∞)
Rozważamy przypadki
1/ x∊(1,∞) i y∊(1,∞) to: logyx>1 ⇒ y<x −−− rys wyżej
2/ x∊(1,∞) i y∊(0,1) to logyx<1 ⇒ y>x −− sprzeczność
3/ x∊(0,1) i y∊(1,∞) ........ sprzeczność
4/ x∊(0,1) i y∊(0,1) ........ sprzeczność
 y = 2−2 ; x = 2−1
logx(logyx) = −log2(log22 2) = −log2(0.5*log22) = −log2 2−1 = 1 > 0
y = 2−2 ; x = 2−1
logx(logyx) = −log2(log22 2) = −log2(0.5*log22) = −log2 2−1 = 1 > 0
 4/ logyx<1 ⇒ y>x
Teraz pasuje ?
4/ logyx<1 ⇒ y>x
Teraz pasuje ?  Dobranoc
Dobranoc 


 Jasne,że y<x ( to wpływ późnej pory prawie 3:00
Jasne,że y<x ( to wpływ późnej pory prawie 3:00 
