Prawdopodobieństwa warunkowe i niezależne. Kasia: Cześć Otóż mam takie małe zadanko do rozwiązania: Dane P(A') = 1/3 P(B) = 1/2 P(A\B)=1/2 Oblicz P(A U B) Więc obliczyłam P(A) = 2/3 Z wzoru P(A/B) = P(A U B)/P(B) Obliczyłam P(A ∩ B) = 1 Podstawiłam Do wzoru P(A U B) = 2/3 +1/2 − 1 i wyszło mi że P(A U B) = 1/6 ,ale w odpowiedziach jest 11/12 Byłyby tu ktoś tak miły i powiedział mnie gdzie robię błąd? Bardzo dziękuję

wredulus_pospolitus: co oznacza zapis: P(A U B)/P(B)

wredulus_pospolitus: Jak może wyjść P(AnB) = 1 To jest prawdą tylko jeżeli P(A) = P(B) = P(AuB) = P(AnB) = 1 = P(Ω)

wredulus_pospolitus: Kolejna sprawa ... jak może Ci wyjść P(AuB) < P(A)

wredulus_pospolitus: P(AuB) = P(A) + P(B) − P(AnB) = 1 − P(A') + P(B) − P(AnB) P(A\B) = P(A) − P(AnB) −> P(AnB) = P(A) − P(A\B) ... wyliczasz i podstawiasz do pierwszego wzoru

Kasia: Faktycznie.Gdzieś źle podstawiałam .To w takim razie jak obliczyć P(A ∩ B)?bo jest to potrzebne do obliczenia P(A U B) = P(A)+P(B)−P(A ∩ B)

Kasia: Wszystko jasne ,dzięki

Kasia: P(AnB) = P(A) − P(A\B) = 1/6 podstawiając pod 1 − P(A') + P(B) − P(AnB) dalej nie wychodzi taki sam wynik jak w odpowiedziach czyli 11/12

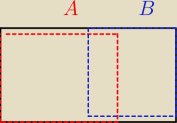
wredulus_pospolitus: P(AuB) = 2/3 + 1/2 − 1/6 = 1 taki wynik powinien wyjść patrz rysunek −−− tylko w takiej sytuacji mamy: P(A) = 2/3 P(B) = 1/2 i P(A/B) = 1/2 zauważ, że: P(A/B) + P(B) = P(A) + P(B) − P(AnB) = P(AuB) <−−− to jest wniosek z naszych przekształceń (i jest to prawdą) A czemu jest to prawdą, ponieważ: A/B −−− cały zbiór A bez tego co ma B B −−− zbiór B więc P(A/B) + P(B) = P(AuB)

Kasia: Tak właśnie taki wynik mi wyszedł.Musi być błąd w książce.Dziękuję za tak rozbudowaną odpowiedź