Przekroje - stereometria
Patryk: Cześć,
Czy mógłby mi ktoś pomóc z zaznaczeniem 3 przekrojów w ostrosłupie prawidłowym czworokątnym?
Szczególnie te dwa pierwsze. Trzeci próbowałem sam zrobić ale wyszedł trójkąt a powinien
pięciokąt.
1) płaszczyzna zawierająca krawędź boczną i środek rozłącznej z nią krawędzi podstawy
2) płaszczyzna zawierająca krawędź podstawy i środek rozłącznej z nią krawędzi bocznej
3) płaszczyzna zawierająca środek wysokości oraz środki dwóch sąsiednich krawędzi podstawy
22 lut 14:47
Blee:
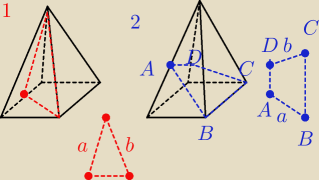
To NIE SĄ trójkąt równoramienny i trapez równoramienny

22 lut 15:00
Blee:
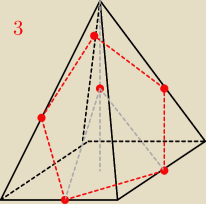
22 lut 15:05
Patryk: Dzięki wielkie! Mam pytanie, skąd mam wiedzieć jak np. wyznaczyć płaszczyznę 2), wiem że
zawiera krawędź podstawy i środek krawędzi bocznej, to nie mógłbym po prostu połączyć krawędzi
ze środkiem i wyszedł by trójkąt? Bo z opisu to trochę ciężko było by się zorientować, że
trzeba 4 wierzchołek dołożyć i wychodzi trapez.
22 lut 15:14
Mila:
Ad (2) Wyobraź sobie ciasteczko o takim kształcie i chcesz go przekroić tak ,
aby cięcie "szło " przez BC i środki dwóch krawędzi bocznych przeciwległych.
22 lut 16:34
Blee:
Miluś ... konsultacja −−− to jednak będzie trapez równoramienny, prawda ?!
22 lut 16:36
Patryk: Chyba równoramienny, przynajmniej tak mam podane w odpowiedziach

22 lut 17:15
Mila:
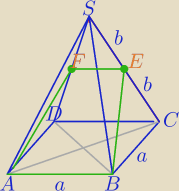
ABEF−trapez równoramienny.
22 lut 17:46
 To NIE SĄ trójkąt równoramienny i trapez równoramienny
To NIE SĄ trójkąt równoramienny i trapez równoramienny 


 ABEF−trapez równoramienny.
ABEF−trapez równoramienny.