marcin help marcin: Wyznaczyć równania stycznych do wykresu funkcji f danej wzorem f(x)=x³−3x²+1, które przechodzą przez punkt P(2,−4).

salamandra: pochodna, pozniej zastosuj wzór na styczną do wykresu funkcji

Jerzy: W jakim punkcie ?

Des: f(x) = x³ − 3x² + 1 P(x_p , y_p)

	f(x0) − yp
f '(x0) = 3x02 − 6x0 =
	x − xp

−−−−−−−−−−−−−−−−−−−−−−−−− y = x³ − 3x² + 1

	y + 4
3x2 − 6x =
	x − 2

2 równania, 2 niewiadome, wyznaczaj punkty

Jerzy: Trzecia linijka od dołu,w mianowniku: x₀ − x_p

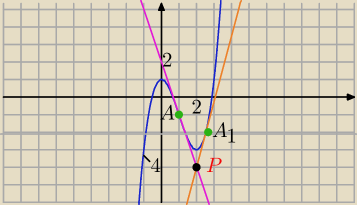
Mila: wg wskazówek Des f(x) = x³ − 3x² + 1 P=(2,−4) f(2)=3 Punkt P∉do wykresu f(x) 1) f '(x)=3x²−6x P=(2,−4), A=(x₀,y₀) 2)

	y0+4
a=
	x0−2

a=f '(x₀)=3x₀²−6x₀ 3)

y0+4
	=3x02−6x0
x0−2

x₀³−3x₀²+1+4=(3x₀²−6x₀)*(x₀−2)

	5
x0=1 lub x0=
	2

	5		17
A=(1, −1) lub A1=(		,−		) − punkty styczności
	2		8

4) Styczne: AP: y=−3x+2

	15
A1P: y=		x−9
	4

================