aksjomat Wolfik: Wyznacz wszystkie wartości parametru m, dla których cztery różne pierwiastki równania x⁴−10x²+m=0 tworzą ciąg arytmetyczny. niech: x²=t i t≥0 x²−10x+m=0 Δ=100−4m

Jerzy: t² − 10t + m = 0 I teraz to równanie musi mieć dwa różne pierwiastki dodatnie.

Wolfik: Δ>0 t₁t₂>0 t₁+t₂>0

Wolfik: Δ=100−4m jaki będzie pierwiastek z delty? c/a>0⇒m>0 t1+t2>0⇒t∊R

Jerzy: Koncentruj się troszkę: t1 + t2 > 0 ⇒ m ∊ R ( parametr m nie ma wpływu na tą sumę ) 100 − 4m > 0 ⇔ m < 25 Ostatecznie: m ∊ (0,25)

Wolfik: co dało mi to, że m∊(0,25)?

Jerzy: To tylko załozenie i oznacza, że tylko w tym przedziale szukasz rozwiązań zadania.

Wolfik: w takim razie do liczę dalej?

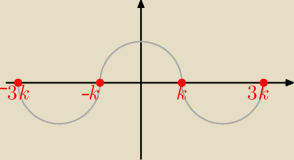
a@b: Proponuję tak: x⁴ −10x²+m=0 −−− funkcja z lewej strony parzysta więc pierwiastki tego równania układają się symetryczne względem osi Oy ( jak na rys) i tworzą ciąg arytmetyczny to można je oznaczyć jako : −3k,−k, 3k, k zatem (x+3k)(x−3k)(x+k)(x−k) =0 ⇒ ................. x⁴−10k²x²+9k⁴=0 i x⁴−10x²+m=0 to 10k²=10 i 9k⁴=m k²=1 to k⁴=1 więc m=9 Odp: m=9 =======

Patryk: A dlaczego różnica ciągu to 2k?

a@b: No, bo tworzą ciąg arytmetyczny

Patryk: Nie o to chodzi dlaczego "2k" a nie jakiś inny zapis np. 'k' ? Z czegoś to wynika?

a@b: Sprawdzamy : dla m=9 mamy równanie x⁴−10x²+9=0 ⇒ (x²−9)(x²−10 ⇒ (x−3)(x+3)(x−1)(x+1)=0 pierwiastki tego równania to, −3,−1,1,3 −−− tworzą ciąg arytmetyczny r= 2 i wszystko gra

Wolfik: dziękuję

a@b: