aksjomat Wolfik: Niech f(x)=1+x+x²+x³+... będzie sumą szeregu geometrycznego zbieżnego. Udowodnij, że zbiorem wartości funkcji f jest przedział (1/2,+∞) |q|<1

	1
1+x+x2+x3+...=Sn⇒f(x)=		, q=x
	1−x

co dalej?

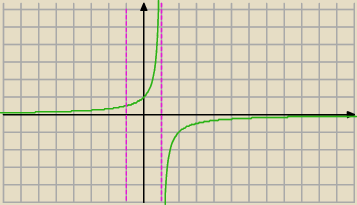
Jerzy: Widzisz " co dalej ? " Jakie wrtości przyjmuje ta funkcja w różowym przedziale (−1,1) ?

Jerzy: A algebraicznie: policz sobie granice f(x) przy x → −1 oraz przy x → 1⁻¹

Wolfik: dla (−1,1) zwf=(1/2,+∞) dlaczego rozpatrujemy tylko przedział (−1,1), a nie (−∞,1)U(1,+∞)?

Jerzy: |q| < 1 , czyli |x| < 1

Wolfik: dziękuję