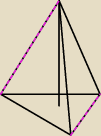
 Dwie skośne względem siebie krawędzie ostrosłupa trójkątnego mają dlugosc równą b, pozostałe
krawędzie mają długość równą a. Oblicz objętość ostrosłupa.
Te skośne to będą te czerwone?
Dwie skośne względem siebie krawędzie ostrosłupa trójkątnego mają dlugosc równą b, pozostałe
krawędzie mają długość równą a. Oblicz objętość ostrosłupa.
Te skośne to będą te czerwone?

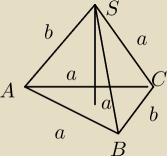 Dobra mam tak
z tw. Pitagorasa w ΔABC
Dobra mam tak
z tw. Pitagorasa w ΔABC
| 1 | ||
( | b)2+h2=a2 (zauważam, że to równoramienny) | |
| 2 |
| 1 | ||
h2=a2− | b2 | |
| 4 |
| 1 | 4a2−b2 | √4a2−b2 | ||||
h=√a2− | b2 = √ | = | ||||
| 4 | 4 | 2 |
| b*√4a2−b2 | ||||||||||||
Pp= | = | ||||||||||||
| 2 | 4 |

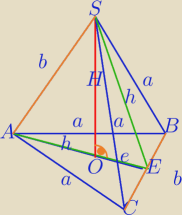 cd. Twoich obliczeń
|OE|=e
1) Tw. Pitagorasa dwa razy: w ΔSOE i ΔSOA
H2=h2−e2
b2=H2+(h−e)2⇔H2=b2−(h−e)2
Porównanie:
b2−(h−e)2=h2−e2
oblicz e
2) Jeszcze raz tw. P. W SOE
cd. Twoich obliczeń
|OE|=e
1) Tw. Pitagorasa dwa razy: w ΔSOE i ΔSOA
H2=h2−e2
b2=H2+(h−e)2⇔H2=b2−(h−e)2
Porównanie:
b2−(h−e)2=h2−e2
oblicz e
2) Jeszcze raz tw. P. W SOE
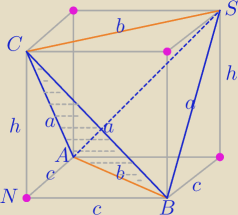 Objętość czworścianu ABCS= V prostopadłościanu − objętość 4 naroży
Vpr.=c2*h
Objętość czworścianu ABCS= V prostopadłościanu − objętość 4 naroży
Vpr.=c2*h
| 1 | 1 | 1 | ||||
VABCS=c2*h−4* | * | c2*h= | c2*h | |||
| 3 | 2 | 3 |
| b | ||
b=c√2⇔c= | ||
| √2 |
| 1 | b | |||
VABCS= | *( | )2*√a2−b2/2 | ||
| 3 | √2 |
| b2*√4a2−2b2 | ||
VABCS= | ||
| 12 |
| 1 | ||
e= | b2−h | |
| 2 |
| √4a2−b2 | 1 | √4a2−b2 | ||||
H2=( | −( | b2− | ))* | |||
| 2 | 2 | 2 |
| √4a2−b2 | 1 | √4a2−b2 | ||||
( | +( | b2− | )) | |||
| 2 | 2 | 2 |
| 2h2−b2 | ||
e= | ||
| 2h |
| 2a2−(1/2)b2−b2 | ||
e= | ||
| √4a2−2b2 |
| 2h2−b2 | ||
e= | ||
| 2h |
| 2h2−b2 | ||
( | )2+H2=h2 | |
| 2h |
| 4h4−4b2h+b4 | |
+H2=h2 | |
| 4h2 |
| 4h4−4b2h+b4 | ||
H2=h2− | ||
| 4h2 |
| 4h4−4h4−4b2h+b4 | ||
H2= | ||
| 4h2 |
| −4b2h+b4 | ||
H2= | ||
| 4h2 |
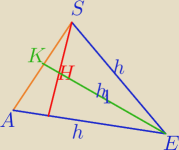 Tradycyjnie prościej będzie obliczyć PAES na dwa sposoby i porównać;
h masz obliczone;
h2=a2−b2/4
h=√a2−b2/4
h1=√h2−b2/4
Tradycyjnie prościej będzie obliczyć PAES na dwa sposoby i porównać;
h masz obliczone;
h2=a2−b2/4
h=√a2−b2/4
h1=√h2−b2/4
| 1 | 1 | ||
*b*√h2−b2/4= | *h*H | ||
| 2 | 2 |
| b*√a2−b2/2 | ||
H= | ||
| √a2−b2/4 |
 Pozdrawiam niestrudzoną Milę
Pozdrawiam niestrudzoną Milę 
 Dziękuję .Też pozdrawiam. Na maturę salamandra ma z naszą pomocą osiągnąć
szczyt formy.
Dziękuję .Też pozdrawiam. Na maturę salamandra ma z naszą pomocą osiągnąć
szczyt formy.
| b | b2 | b2 | b | |||||
PAES= | √(a2− | − | )= | √4a2−2b2 | ||||
| 2 | 4 | 4 | 4 |
| 1 | b | b | b2 | |||||
V=2* | * | * | √4a2−2b2}= | √4a2−2b2 | ||||
| 3 | 2 | 4 | 12 |
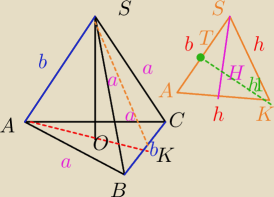
 Zwykle wpisuję w prostopadłościan.
A jak będzie wg Ciebie , gdy krawędzie skośne parami równe?
a,a, b,b, c,c
Ja obliczę po wpisaniu w prostopadłościan o krawędziach ( x,y, z) różnej długości.
Zwykle wpisuję w prostopadłościan.
A jak będzie wg Ciebie , gdy krawędzie skośne parami równe?
a,a, b,b, c,c
Ja obliczę po wpisaniu w prostopadłościan o krawędziach ( x,y, z) różnej długości.

| 1 | ||
( | b)2+h2=a2 | |
| 2 |
| 1 | |
b2+h2=a2 | |
| 4 |
| 1 | ||
h2=a2− | b2 | |
| 4 |
| 1 | √4a2−b2 | |||
h=√a2− | b2 = | |||
| 4 | 2 |
| 1 | ||
( | b)2+h12=h2 | |
| 2 |
| 1 | 1 | ||
b2+h12=a2− | b2 | ||
| 4 | 4 |
| 1 | ||
h12=a2− | b2 | |
| 2 |
| 1 | ||
h1=√a2− | b2 | |
| 2 |
| 1 | 1 | |||
P1= | *b*√a2− | b2 | ||
| 2 | 2 |
| 1 | 1 | |||
P2= | *h*H= √a2− | b2*H | ||
| 2 | 4 |
| 1 | 1 | 1 | 1 | ||||
*b*√a2− | b2= | *h*H= √a2− | b2*H | ||||
| 2 | 2 | 2 | 4 |
| 1 | 1 | 1 | 1 | ||||
*√a2− | b2*H= | *b*√a2− | b2 / * 2 | ||||
| 2 | 4 | 2 | 2 |
| |||||||||||
H= | |||||||||||
|
| |||||||||||
Pp= | |||||||||||
| 2 |
| 1 |
|
| ||||||||||||||||||||||
V= | * | * | = | |||||||||||||||||||||
| 3 | 2 |
|
| 1 | 1 | 1 | √4a2−2b2 | 1 | ||||||
= | b2*√a2− | b2 = | *b2* | = | b2√4a2−2b2 | |||||
| 6 | 2 | 6 | 2 | 12 |

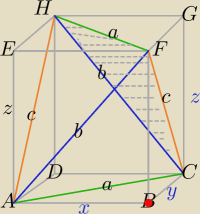 Objętość czworościanu równościennego o krawędziach skośnych parami równych:
a,a, b,b, c,c .
VABCDEFGH=x*y*z
Objętość czworościanu równościennego o krawędziach skośnych parami równych:
a,a, b,b, c,c .
VABCDEFGH=x*y*z
| 1 | 1 | 1 | ||||
VnarożaAFCB= | * | xyz= | xyz | |||
| 3 | 2 | 6 |
| 1 | 1 | |||
VHFCA=xyz−4* | xyz= | xyz | ||
| 6 | 3 |
| c2+b2−a2 | ||
z2= | ||
| 2 |
| a2+b2−c2 | ||
x2= | ||
| 2 |
| a2+c2−b2 | ||
y2= | ||
| 2 |
| √(c2+b2−a2)*(a2+b2−c2)*(a2+c2−b2) | ||
VHFCA= | ||
| 6√2 |