Równanie Szkolniak:

	1
Rozwiąż równanie: 2−|x|=		(|x+1|+|x−1|)
	2

Jakieś wskazówki? Rozpatrzeć czterema przedziałami?

Blee: f(x) = 2^−|x|

	|x+1| + |x−1|
g(x) =
	2

poniekąd, ale wystarczy zauważyć, że: 1) dla x< −1 g(x) to funkcja malejąca, g(x) to funkcja liniowa g(−1) = 1 2) dla x∊<−1;1> g(x) jest funkcją stałą 3) dla x>1 g(x) jest funkcją rosnącą, g(x) to funkcja liniowa oczywiście, g(1) = 1 natomiast należy zauważyć, że f(x) = e^−|x| ≤ e⁰ = 1 w związku z tym jedynie dla f(x) = 1 może zajść równość f(x) = g(x) natomiast f(x) = 1 ⇔ x = 0

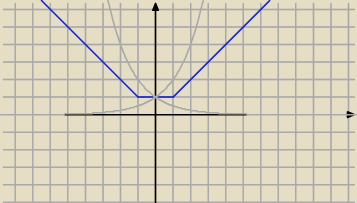
Jerzy: Dla x < 0 lewa część szarego wykresu Dla x ≥ 0 prawa Rozwiązanie: x = 0

Blee: ewentualnie (dobrze by było) zapisać g(x) w postaci klamerkowej (tak dla jasności tego co napisałem)

Szkolniak: wszystko jasne, dziękuje!

Mila: Podpowiedź:

	1		|x+1|+|x−1|
(		)|x|=
	2		2

	1
f(x)=(		)|x|
	2

f(0)=1− największa wartość f(x)

	|x+1|+|x−1|		|x+1−x+1|
g(x)=		≥		=1
	2		2

równość g(x)=1 x∊<−1,1> odp. x=0