ekstrema lokalne- problem narysowaniem wykresu patrykk559: 2.95 Wyznacz ekstrema lokalne funkcji

	1		1
b) f(x)=		x4−02x3+4		x2+7
	4		2

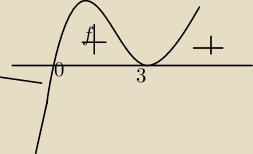
f`(x) = 0 wychodzi x(x²−6x+9) = 0 funckcja prezentuje się mniej więcej tak jak na rysunku. Mógłby mi ktoś wytłumaczyć dlaczego w przedziale (−nieskończkoność,0) funcja jest malejąca?

jc: To wykres pochodnej.

ruszamy: Odwieczny problem. Otóż "wężyk" to tylko wizualizacja wykresu pochodnej. Widzimy, że dla ujemnych argumentów pochodna jest mniejsza od zera. A więc oznacza to tyle, że w tym przedziale funkcja pierwotna jest malejąca. Innymi słowy: informacja jaką dostajemy mówi nam o tym, na jakim przedziale funkcja maleje, rośnie.