stereometria
salamandra: Na trzech półprostych parami prostopadłych nie zawierających się w jednej płaszczyźnie i
wychodzących z punktu A, odmierzono odcinki AM,AN i AP takie, że AM=AN=a i AP=2a.
Znajdź odległość punktu A od płaszczyzny MNP.
Nie bardzo wiem jak zrobić rysunek czegoś takiego
19 lut 15:13
ite: Sprawdź "Regułę lewej dłoni"
19 lut 15:23
19 lut 15:24
ite: Tak, te kolorowe półproste spełniają warunek:
Na trzech półprostych parami prostopadłych nie zawierających się w jednej płaszczyźnie i
wychodzących z punktu A, ...
19 lut 15:29
salamandra:
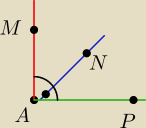
Nie rozumiem tego pojęcia "parami prostopadłych", z tego wynikałoby, że każda para musi być
prostopadła do drugiej, a tutaj kąt prosty jest tak jak na rysunku, czy ja coś mylę?
19 lut 15:32
19 lut 15:34
Des:
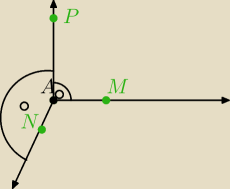
19 lut 15:35
Des: Kółka to kąty proste, nawet wyszło
19 lut 15:35
salamandra: Tak, właśnie tak to sobie wyobrażałem, jest tak, jak zapisałaś?
19 lut 15:36
ite: 
i artystycznie i kubistycznie!
19 lut 15:36
ite: to artystycznie było do Des
19 lut 15:37
salamandra: A do mnie?
19 lut 15:43
ite: salamandra zależności takie jak 15:34
RysunekDes idealny, połącz pkty M,N,P, otrzymasz graniastosłup o podstawie trójkąta.
19 lut 15:44
Mila:
Bardzo ładne zadanko
19 lut 15:47
Mila:
ite− ostrosłup i to ciekawy.
PMNA
19 lut 15:50
ite: oryginalne, na pomyślenie,
Podpowiedź Milu dalej, ja niestety muszę wracać do swoich zajęć.
19 lut 15:52
ite: oczywiście ostrosłup
19 lut 15:53
salamandra: Tak, poprosiłem nauczyciela o zadania z jego jak ja to nazywam "Księgi Mądrości"
no
potrzebuję niestety podpowiedzi, bo nie wyobrażam sobie jak z tego ma powstać ostrosłup, gdy
połączę MNP, to przecież powstanie mi razem z A jakiś czworokąt, bo tak to musiałbym lecieć po
linii prostej, żeby to był trójkąt?
19 lut 15:54
salamandra:
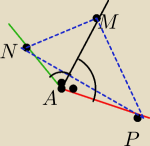
coś takiego?
19 lut 16:02
salamandra: Chociaż nie, wróć− nie rozumiem jednego warunku− jakim cudem AN może być prostopadłe do AM?
19 lut 16:04
salamandra: Na rysunku Desa
19 lut 16:04
ite: spójrz w róg pokoju: tam będzie pkt A,
wychodzą z niego trzy linie
te dwie łączące podłogę ze ścianami przechodzą przez pkt N i M
w górę idzie łączenie ścian, tam będzie pkt P
ostrosłup tworzą trzy trójkąty prostokątne (w tym dwa przystające, trzeci jest równoramienny w
podstawie) i jeden bez kąta prostego, równoramienny
19 lut 16:38
salamandra:
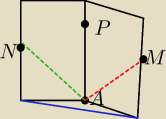
coś takiego? (założmy że na rysunku są dwie ściany, a to niebieskie tam to podłoga)
19 lut 16:59
Mila:
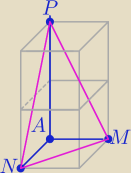
Teraz widzisz?
19 lut 17:15
salamandra: a one nie miały leżeć na innych płaszczyznach? AN i AM nie leżą na wspólnej płaszczyźnie?
19 lut 17:25
Mila:
Parami leżą w jednej płaszczyźnie.
Przez AN i AM i AP nie poprowadzisz płaszczyzny.
19 lut 17:39
salamandra: aha, no to w tym momencie to jest o 1000 razy łatwiejsze.... już dawno bym poprowadził tak jak
Ty, ale myślałem, że parami również nie mogą być, stąd to moje zagmatwanie. Dziękuję Ci
Będę za godzinę rozwiązywał.
19 lut 17:47
salamandra:
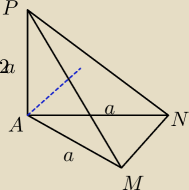
ta szukana odległość to jakoś tak? i tam będzie kąt prosty?
19 lut 19:17
salamandra:
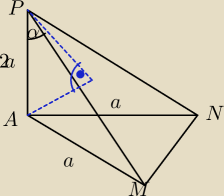
(2a)
2+a
2=PM
2
PM=a
√5 = PN
próbowałem wyznaczyć sinα, bo myślałem, że to będzie ten sam kąt, ale teraz sobie uświadomiłem,
że ten kąt α, to odnosi się tylko do trójkąta APM,
ale napiszę, może się o dziwo do czegoś przyda
a
√5*sinα=a
19 lut 19:39
ite: Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź AP i środek odcinka MN.
Wtedy szukana odległość nie będzie taka "zawieszona" w powietrzu.
19 lut 19:43
salamandra:
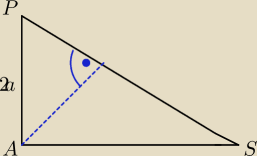
S− środek boku MN
i co dalej?
19 lut 19:54
ite: wszystkie boki tego trójkąta znasz / możesz obliczyć
pozostaje wyliczyć jego wysokość
19 lut 20:01
Mila:
Pomyliłam się.
Zaraz podpowiem.
19 lut 20:06
salamandra: Oh.....
zapomniałem że ∡MAN= 90 stopni..... zaraz spróbuję jeszcze sam, zanim przeczytam
do końca Twoje Milu
19 lut 20:06
salamandra: | | 2 | |
Nie pomyliłaś się, w odpowiedzi jest |
| a |
| | 3 | |
19 lut 20:06
Mila:
wpisz w wyszukiwarkę Mila to bedzie tam rozwiązanie.
19 lut 20:10
salamandra: H− wysokość ostrosłupa opuszczona z P na MNP tego nie rozumiem, nie powinno być z A?
19 lut 20:12
Mila:
Właśnie powinno być :
H− wysokość ostrosłupa opuszczona z punktu A na podstawę MNP .
19 lut 20:14
salamandra: Mam tak:
W ΔAMN
MAN=90 stopni
więc |MN|
2=a
2+a
2 ⇒ |MN|=a
√2
2) WΔASM
3) w ΔAPS
| | 9 | | 9 | | 3a√2 | |
|PS|= √ |
| a2 = a√ |
| = |
| |
| | 2 | | 2 | | 2 | |
Ok, mam wysokość PS, ale nadal nie wiem jak dojść do wysokości szukanej?
19 lut 20:30
salamandra: Dobra, już chyba rozumiem− najpierw liczę objętość ostrosłupa tak jakby AMN było podstawą, więc
V=P
AMN*2a*{1}{3}
| | 1 | | 1 | |
V= |
| a2*2a*{1}{3} = |
| a3 |
| | 2 | | 3 | |
A teraz liczę objętość tak jakby PMN bylo podstawą, a szukany odcinek wysokością?
więc
| | 3a√2 | | 1 | | 3 | |
PPMN= a√2* |
| * |
| = |
| a2 |
| | 2 | | 2 | | 2 | |
| 1 | | 3 | | 1 | |
| a3= |
| a2*H* |
| / * 3 |
| 3 | | 2 | | 3 | |
19 lut 20:38
Mila:
ΔMNP jest Δrównoramiennym.
19 lut 20:39
salamandra: i co wynika z tego, że MNP jest równoramienny?
19 lut 20:51
Mila:
ŁĄtwo obliczyć wysokość w tym Δ i potem pole.
19 lut 21:37
salamandra: Czyli objąć tę strategię co zrobiłem z 20:30?
Rozumiem że nie ma innego sposobu żeby wyliczyć tę odległość oprócz przyrównania V?
19 lut 21:38
Mila:
Najłatwiej z porównania objętości.
19 lut 21:43
salamandra: No wyszło, zauważyłem, że robię ostatnio mniej zadań, a spędzam nad tym więcej czasu....
19 lut 21:54
Kacper:
Jak się╚ robi trudniejsze zadania, to tak jest
21 lut 10:16
Mila:
Kacper Rzadko się pojawiasz
Zapracowany?
21 lut 19:10
