funkcja kwadratowa Esssssa: f(x)=2x²+20x+48 a)wyznacz pozostale postacie funkcji b)narysuj wykres c)odczytaj wlasnosci f(x−48), f(x) < −3 d)wyznacz argumenty dla ktorych wartosci f(x) i g(x)=5x²+11x+36 sa rowne e)wyznacz argumenty dla ktorych wartosci funkcji f(x) sa mniejsze od wartosci h(x)=6x²+31x+45 f) wyznacz najwieksza i najmniejsza wartosc funkcji f(x) w przedziale x∊<−7,2)

Esssssa: i wyznacz wspolczynnik a, b i c funkcji f(x) ax²+bx+c jezeli do paraboli bedacej jej wykresem napezy punkt P=(7, −5) a wierzcholkiem paraboli to W=(9,7)

Esssssa: proooosze bardzo mam to na 14:00

zrób _to_sam:

Esssssa: moze komus sprawniej pojdzie 😅

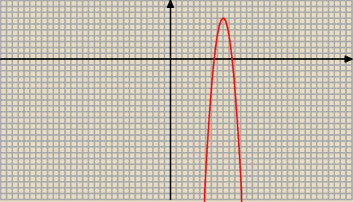
janek191: z.2 f(x) = a x² + b x + c P =(7, − 5) W = ( 9, 7) ⇒ p = 9 i q = 7 zatem f(x) = a*(x − p)² + q = a*( x − 9)² + 7 P należy do paraboli ( wykres funkcji f), więc mamy − 5 = a*(7 − 9)² + 7 − 5 = a*(−2)² + 7 − 5 = 4 a + 7 4 a = − 5 − 7 = − 12 / : 4 a = − 3 zatem f(x) = −3*( x − 9)² + 7 = −3*(x² − 18 x + 81) + 7 = −3 x² + 54 x − 243 czyli a = − 3 , b = 54 , c = − 243 ======================

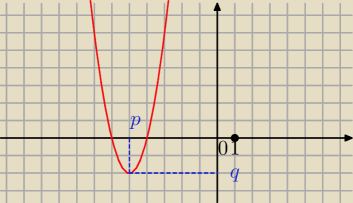
janek191: z.1 f(x) = 2 x² + 20 x + 48 a = 2, b = 20, c = 48

	−b		−20
p =		=		= − 5
	2a		2*2

q = f(p) = f(−5) = 2*(−5)² + 20*(−5) + 48 = 2*25 − 100 + 48 = −2 Postać kanoniczna f(x) = a*(x − p)² + q f(x) = 2*( x + 5)² − 2 ================

janek191: Postać iloczynowa f(x) = a*( x − x₁)*(x − x₂) f(x) = 2 x² + 20 x + 48 a = 2 Δ = b² − 4a*c = 20² − 4*2*48 = 400 − 384 = 16 √Δ = 4

	− b − √Δ		−20 − 4		−24
x1 =		=		=		= − 6
	2a		2*2		4

	− b + √Δ		− 20 + 4
x)2 =		=		= − 4
	2 a		4

f(x) = 2*( x + 6)*( x + 4) − postać iloczynowa ==================

janek191: b) Wykres jest narysowany wyżej.

janek191: d) f(x) = g(x) 2 x² + 20 x + 48 = 5 x² + 11 x + 36 3 x² − 9 x − 12 = 0 / : 3 x² − 3 x − 4 = 0 ( x +1)*(x − 4) = 0 Odp. x = − 1 lub x = 4 =====================