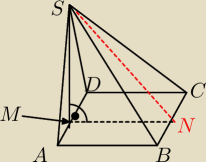
stereometria salamandra: Podstawą ostrosłupa ABCDS jest kwadrat. ściana boczna ADS jest prostopadła do płaszczyzny podstawy oraz AB=12, AS=SD=10 Oblicz a) objętość ostrosłupa b) pole Pb powierzchni bocznej ostrosłupa Pp=144 6²+h²=10² h=8

	1
V=		*144*8 = 384
	3

	1
b) PΔADS=		*12*8 = 48
	2

PΔABS − nie wiem jak wyznaczyć wysokość tego trójkąta PΔBSC t− wysokosc SM²+12²=SN² 64+144=SN² 208= SN² SN=√208 = 4√13

	1
PΔBSC=		*12*4√13 = 24√13
	2

PΔSDC BN=6 BN²+SN²=SB² 36+208=SB² SB=2√61 = SC AS=10, AB=12, SB=2√61− zostaje wzór Herona? bo wysokość nie podzieli mi na połowę podstawy

a@b: kąty BAS i CDS −−−− kąty proste !

salamandra: wiedziałem..

a@b: to ściany BAS i CDS −−− trójkąty prostokątne przystające! i po ptokach

a@b: Co wiedziałeś?

salamandra: Tak, to już wiem, że przystające. rozumiem, że nie ważne jaką prostą poprowadziłbym z AD, to będzie ona prostopadła?

salamandra: domyślałem się, że tam muszą być proste, bo "wzrokowo" już widziałem niedawno identyczny rysunek, gdy Ty lub Mila mi coś tłumaczyliście o rzutach bodajże.

salamandra: tłumaczyłyście*

salamandra: Pb= 60+60+24√13+48= 168+24√13

a@b: Postaw sobie trójkątną kartkę na kwadratowej tekturce zobaczysz kąty proste

salamandra: Taa, wystarczyło, że przekręciłem telefon patrząc na swój rysunek wyżej