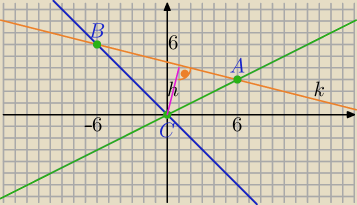
Geometria analityczna Patryk: Witam, Mam policzyć pole figury ograniczonego nierównościami: x + y ≥ 0 x − 2y ≤ 0 x + 4y − 18 ≤ 0 Wychodzi trójkąt Wyjdzie jeden wierzchołek to C=(0;0), dwa pozostałe to A=(6,3) i B=(−6;6) AB = √153

	37√17
odległość C od prostej AB =		−−> wysokość trójkąta
	17

Pole wychodzi mi 55,5 ale w odpowiedziach mam 27. Gdzie popełniłem błąd?

Saizou : Punkt B masz źle policzony

jc: Zastosuj lepiej prosty wzór na pole równoległoboku rozpiętego przez wektory (a,b), (c,d). Pole = |ad−bc| Pole trójkąta = pole równoległoboku /2 P=[6*6−(−6)*3]/2=27

Patryk: Kurczę, chyba ślepy jestem to nie widzę błędu w tym puncie B

jc: Punkty masz dobrze wyznaczone. Tylko potem komplikujesz, a wzór na pole jest prosty.

Patryk: Wolałbym skorzystać z metod poznanych w szkole średniej Ale bez kitu, sprawdziłem obliczenia i powinno wyjść dobrze, pole = 1/2 * AB * H

Saizou : Przeprasza, źle wklepałem do geogebry wprowadziłem prosta y=x

Mila: Wzór podany 20:12 masz podany w szkole średniej C=(0,0), A=(6,3), B=(−6,6) Wg wzoru 20:33 |AB|=√12²+3²=√153=3√17 h=Odległości punktu C od prostej k: x + 4y − 18 =0

	|0+4*0−18|		18
h=d(C,k)=		=
	√1+42		√17

	1		18
PΔ=		*3√17*		=27
	2		√17

Patryk: Oo dzięki wielkie, już znalazłem błąd. Zależy w jakiej szkole średniej, ja dla przykładu nie miałem tego wzoru a to, ze powinien być to już inna sprawa. Wiele rzeczy powinno się pojawiać na lekcjach a zawsze brakuje czasu...

Mila: Lepiej będzie jak się nauczysz , przydaje się i jest krócej. CA→=[6,3] CB^→=[−6,6] −−−−−− 6 3 −6 6 −−−−−− W=6*6−3*(−6)=36+18=54

	1
PΔ=		*|54|=27
	2

Patryk: A jak to jest z tym wzorem, potrzebne są tylko dwa wektory? A trzeci nie? Żeby wiedzieć gdzie obszar figury się kończy.

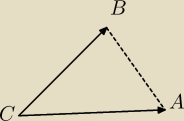
jc: Wektory możesz poprowadzić również od A lub od B.

Patryk: A jeszcze jedno pytanko, czy zna ktoś program w którym mógłbym wpisać nierówności a program pokaże mi obszar określony przez te nierówności? Przydałby sie taki do ćwiczeń

Saizou : geogebra

Mila: Możesz wpisać w wolfram tak: x + y ≥ 0 ,x − 2y ≤ 0, x + 4y − 18 ≤ 0