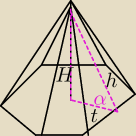
stereometria salamandra: Do sprawdzenia dwa zadanka: Pole podstawy ostrosłupa prawidłowego sześciokątnego jest równe 96√3, miara kąta nachylenia ściany bocznej do płaszczyzny podstawy jest równa 30 stopni. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

	a√3
t=
	2

Pp=96√3

	a2√3
Pp=6*
	4

384√3=6a²√3 6a²=384 a²=64 a=8 t= 4√3

	H
tg30 =
	t

√3		H
	=
3		t

√3		H
	=
3		4√3

H=4

	t
cos30 =
	h

√3		4√3
	=
2		h

8√3= h√3 h=8

	a*h		8*8
Pb= 6*		= 6*		= 6*32 = 192
	2		2

	1
V=		*96√3*4 = 32√3*4 = 128√3
	3

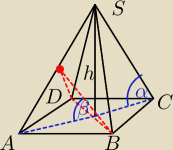
Zad 2. Ostrosłup prawidłowy czworokątny o wysokości długości h tworzącej z krawędzią boczną kąt α, przecięto plaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem β. gdzie β < 90. Oblicz pole przekroju przyjmując, że h jest mniejszym pierwiastkiem równania. Ten przekrój to będzie trapez? Zaraz postaram się dodać swój rysunek.

ite: zad. 2 https://www.geogebra.org/3d/neejkrse

salamandra: no przecież...................... dziękuję

ite: jeszcze dodam model w którym przekrojem będzie trapez https://www.geogebra.org/3d/brakdewj

Mila: ite jak zwykle niezawodna z geogebrą

salamandra: Zad 2. tgα= U{h}{a√2 h=tgα*a√2

h
	=a√2
tgα

	h√2
2a=		/ : 2
	tgα

	h√2
a=
	2tgα

	h
P=		*H
	tgα

H− wysokość czerwonego trójkąta (przekroju) Nie wiem co dalej

salamandra:

	h		1
P=		*H*		oczywiście
	tgα		2

Mila: O jakie równanie chodzi w treści?

salamandra: Myślałem, że to cała treść zadania, przyznam, że mam tylko zdjęcie, być może kawałek treści się ucięło https://imgur.com/a/KLrdzcM

a@b: Zły kąt α zaznaczyłeś! Ma być między h i krawędzią boczną wierzchołek kąta α to S

salamandra: aha , no to zamieniam na ctg i po problemie

a@b: Jaką masz odp do tego zadania ( napisz)

salamandra: Nie mam niestety, mam tylko to zdjęcie co wysłałem wyżej. Zrobiliśmy na lekcji zdjęcie, bo tylko nauczyciel ma tę akurat książkę

Mila: To skonsultuj jutro dalszą część treści

Mila: I popraw rysunek, jak napisała Eta.

a@b: Mila ja mam taki wynik:

	√2H2tgα sinα
P=
	cos(β−α)

===================

a@b: <A może Bogdan się skusi Wysyłam ... niczym Ewa w raju

salamandra: Generalnie to równanie to było:

	n 3		n+2 4
5*		=

nauczyciel się nie skapnął, że był symbol Newtona, który przede mną, ale wyjaśnił nam na szybko.

	12		4
Dany był jeszcze sinα=		i cosβ=
	13		5

	161
Wynik to P=
	7

salamandra: Rozwiązaliśmy to zadanie na lekcji, ale podaję dla a@b wynik

a@b: No i mam dobrze ( bo przypadkowo wpisał mi się √2 Powinno być

	H2tgα *sinα
P=
	cos(β−α)

i teraz jak podałeś:..... H=3, sinα=12/13 , tgα=12/5 i cosβ=4/5 Mi wychodzi takie pole

	162
P=
	7

a@b: Ja czekaaaaaaaaaaaaaaaaaaam na odzew !

salamandra: Być może 162, nie zdążyłem zapisać, bo robiłem to na tablicy

a@b:

	162
Poprawna odp:
	7

czyli w/g tego wzoru który podałam o 00:11 tylko bez √2

salamandra: Tak, 162. Podziwiam, że bez tych danych to zrobiłaś

a@b: Kiedyś.... dawno, dawno temu rozwiązywało się takie zadanka tylko na "literkach" a na koniec podstawiało się konkretne dane zamiast literek Powodzenia